doi: 10.56294/sctconf2024.1107

Category: STEM (Science, Technology, Engineering and Mathematics)

CASE REPORT

A computational model of epidemics using seirx model

Un modelo computacional de epidemias utilizando el modelo seirx

Senbagavalli Marimuthu¹ *, Saswati Debnath¹ *, Saravanakumar Ramachandran² *, Manikandan Parasuraman² *, Satish Menon³ *

¹Alliance University, Department of CSE. Bangalore, Karnataka, India.

²Jain Deemed to be University, Department of CSE. Bangalore, Karnataka, India.

³SRM University, Faculty of management and commerce. Sonepat, India.

Cite as: Marimuthu S, Debnath S, Ramachandran S, Parasuraman M, Menon S. A computational model of epidemics using seirx model. Salud, Ciencia y Tecnología - Serie de Conferencias. 2024; 3:.1107. https://doi.org/10.56294/sctconf2024.1107

Submitted: 20-02-2024                   Revised: 08-05-2024                   Accepted: 16-08-2024                 Published: 17-08-2024

Editor: Dr. William Castillo-González

ABSTRACT

Epidemiology studies the spread and impact of infectious diseases within defined populations, focusing on factors such as transmission rate, infectious agents, infectious periods, and susceptibility. Computational epidemiology simulates these factors using basic compartmental models like Susceptible-Infected-Recovered (SIR), Susceptible-Exposed-Infected (SEI), and Susceptible-Exposed-Infected-Recovered (SEIR). However, these models inadequately address mortality and fatality rates. To enhance the accuracy of epidemic transmission models, we propose an expanded SEIR model by introducing a new compartment, denoted as X, representing the deceased population. This new model, Susceptible-Exposed-Infected-Recovered-Deceased (SEIRX), incorporates fatality and mortality rates, providing a more comprehensive understanding of epidemic dynamics.  The SEIRX model demonstrates superior accuracy in inferring and forecasting epidemic transmission compared to existing models, offering a complete and detailed approach to studying infectious disease outbreaks.

Keywords: Computational Epidemiology; Susceptible-Exposed-Infected; Forecasting of Epidemics; World Health Organization; Susceptible; Exposed; Infected; Recovered (SEIRX).

RESUMEN

La epidemiología estudia la propagación y el impacto de las enfermedades infecciosas en poblaciones definidas, centrándose en factores como la tasa de transmisión, los agentes infecciosos, los periodos infecciosos y la susceptibilidad. La epidemiología computacional simula estos factores mediante modelos compartimentales básicos como Susceptible-Infectado-Recuperado (SIR), Susceptible-Expuesto-Infectado (SEI) y Susceptible-Expuesto-Infectado-Recuperado (SEIR). Sin embargo, estos modelos no abordan adecuadamente la mortalidad y las tasas de letalidad. Para mejorar la precisión de los modelos de transmisión epidémica, proponemos un modelo SEIR ampliado mediante la introducción de un nuevo compartimento, denominado X, que representa a la población fallecida. Este nuevo modelo, Susceptible-Expuesto-Infectado-Recuperado-Muerto (SEIRX), incorpora las tasas de letalidad y mortalidad, proporcionando una comprensión más completa de la dinámica epidémica.  El modelo SEIRX demuestra una precisión superior en la inferencia y previsión de la transmisión epidémica en comparación con los modelos existentes, ofreciendo un enfoque completo y detallado para estudiar los brotes de enfermedades infecciosas.

Palabras clave: Epidemiología computacional; Susceptible-Expuesto-Infectado; Previsión de epidemias; Organización Mundial de la Salud; Susceptible; Expuesto; Infectado; Recuperado (SEIRX).

INTRODUCTION 

The raw data and comprehensive observational data are not enough to forecast the outbreaks of epidemics. In order to have more accurate and complete picture of transmission dynamics inference of epidemics the computational analysis can be used. Inference and forecasts of the outbreak can be used to make required arrangements of medicines and medical personnel. Mathematical modeling and Bayesian inference have been developed in the area of infectious disease modeling have enabled the assumption of key epidemiological characteristics related with the historical disease outbreaks. The deterministic and stochastic models were employed for both model specification and observational error by providing a better estimate of system behavior than simply analysis using the data or model alone.

Mathematical models can be used to forecast how pathogens progress, the current state, and expected results. These models consider few basic assumptions and mathematics to find factors for various infectious diseases and applies those factors to calculate the effects of possible interventions, like herd immunity and mass vaccination programs. There are three basic types of computational models that are available for infectious diseases which are spread among the defined population by person-to-person. Parameters are estimated and categorized for various kinds of diseases. These parameters are used to identify the herd immunity ratio and vaccination. The mathematical models are presented with notations, concepts, intuition and more refined models.

The SEIRX model is an extension of the classic SEIR (Susceptible-Exposed-Infectious-Recovered) epidemiological model, incorporating additional compartments to represent specific sub-populations or factors influencing disease dynamics. The term "X" typically denotes an extra compartment or a set of additional features beyond the core SEIR structure. The SEIRX model is widely used in infectious disease modeling to provide a more nuanced understanding of epidemic scenarios.

Here's a brief introduction to the key components of the SEIRX model:

Susceptible (S): this compartment represents individuals who are susceptible to the infectious disease but have not yet been exposed.

Exposed (E): individuals in this compartment have been exposed to the pathogen but are not yet infectious. This stage accounts for the latent period between exposure and becoming infectious.

Infectious (I): this compartment includes individuals who are infectious and capable of transmitting the disease to susceptible individuals.

Recovered (R): individuals who have recovered from the infection and gained immunity are placed in this compartment.

X Compartment: the "X" compartment introduces additional complexity to the model. This could represent various sub-populations, such as asymptomatic carriers, hospitalized individuals, or those under specific interventions like vaccination.

Spreading of the epidemics among a defined population has been described by several types of computational models either stochastic or deterministic. The application of these models varies according to the kind of parameters consider and computational methods. The World Health Organization (WHO) observations are considered and are compiled with computational modeling and Bayesian inference to estimate the key characteristics of epidemiology and inference mortality levels and future case for the current Ebola outbreak in West Africa. We collected data of epidemic outbreak of Ebola for a week and used those collected data to assess inference and forecasting model performance.⁽¹⁴⁾

Related work

Ad-hoc balancing palliation solutions aim to maintain a self-balancing business pace after a specified mitigation-free period of time have been developed. They evaluated the impact of several balancing methods in the latter context in light of the COVID-19 outbreak in England and the Brazilian state of Amazonas.⁽¹⁾ For the model under study, two rumour existing-endemic equilibrium points one rumor-free have been developed. Then, using the fuzzy forward Euler and fuzzy nonstandard finite difference (FNSFD) methods, the model is numerically solved⁽²⁾ The findings have significance for academics looking to use scaled populations in their work since they suggest that distinct regional dynamics of the spread of disease are particularly connected with varied population sizes⁽³⁾ During a pandemic, the suggested framework offers regional and national authorities a useful tool for improved public health decisions,⁽⁴⁾ Their findings suggest that healthcare overcapacity will develop when predicted economic effects are greater. But when the illness severity is low and the pandemic's predicted economic losses are high, a no-intervention policy might be preferred. The expense of intervention increases in direct proportion to the infection's severity. Along with the severity of the economic costs of interventions and the rate of illness infection, the death toll also rises. Our models recommend earlier mitigation tactics, often beginning before the healthcare system becomes saturated when illness severity is high⁽⁵⁾ This model explains how infectious diseases spread and how a person can go from being vulnerable to becoming infected and then recovering⁽⁷⁾

The results demonstrate the effectiveness of the two methods, with both achieving classification accuracy levels of over 70 %. Additionally, the trials we ran show how association rule mining can be used and is useful for categorizing images. This model accurately captures Nairobi's STD (Sexually Transmitted Diseases) prevalence and HIV prevalence temporal trend.⁽⁸⁾ They proposed a straightforward technique to model dynamic networks of sex relationships. We study how the duration of infectiousness alters the effective contact network over which disease may spread using survey data on sexual views and lifestyles. Then, we mimic a number of control techniques, including behavioral treatments, immunization, and screening.^(9,10)

The Sustainable Development Goals (SDGs) place a priority on enhancing global health and well-being, as evidenced by their targets to eradicate AIDS, tuberculosis, and malaria epidemics, make important progression in maternal and children health, and combat the rising incidence of non-communicable diseases (NCDs).The primary findings of the Commission's report are that the HIV epidemic is not on course to be eliminated and that the instruments available today are inadequate.  Notwithstanding the fact that anti-retro viral therapy (ART) has altered the immune system's response to HIV by reducing mortality, improving quality of life, and preventing new HIV infections, treatment for HIV itself will not stop the spread of HIV. The UNAIDS 90-90-90 strategy must be backed by a strong serious-mindedness to particular HIV interference that is scaled up, as well as to the creation of a impeding vaccine and a workable HIV cure.⁽¹¹⁾

They developed the SEAIHRDS adaptable mathematical framework, which stands for "Susceptible, E-exposed, A-asymptomatic, I-infected, H-hospitalized, R-recovered, d-dead from COVID-19 infection, S-susceptible." The framework can predict likely epidemic consequences, especially the necessary hospital capacity, and simulate various deployment scenarios for preventive approaches.⁽¹²⁾ For the purpose of digital mammography tumour identification, some tests have been conducted. They looked into the use of several data mining methods, including neural networks and association rule mining, for the identification and classification of anomalies. The outcome demonstrate the effectiveness of the two methods, with both achieving classification accuracy levels of over 70 %. Additionally, they exploited association rule mining's efficiency for image categorization in their tests.⁽¹³⁾ Deep learning algorithms are used for improving health using smart health care management systems and analysis of psychological disorder.^(14,15)

The SIR Model

The Suspected-Infected-Recovered Model is used in epidemiology to figure out the amount of susceptible, infected, recovered people in a define population.

Assumptions

The models can be defines as good when they considers appropriate assumptions. The SIR model considers the basic and appropriate assumptions as follow:

Table 1. List of parameters using in modeling
Parameter/ Notation	Description
S	Number of susceptible individuals
I	Number of infected individuals
R	Number of recovered individuals
α	Probability of becoming infected by a disease
β	Average number of transmissions from an infected person in a time period
η	Case called fatality rate
N	Population size
Z	Average time with which the person becomes infected before exposed
D	Mean infectious period
M	Average time from symptom onset to death
Source: Wise S et al.^(^3)

The basic factors considered in SIR model are susceptible, infected and recovered individuals at time t, for total population size N. The differential equation is given by:

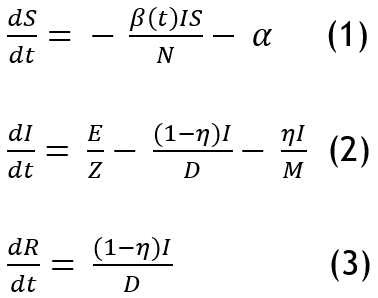
The total population is such a way give as:

Figure 1. General SIR model for epidemics

The figure 1 depicts general model for epidemics. Epidemic models serve as essential tools for explaining and predicting the rate at which infectious diseases spread. These mathematical and computational models are designed to capture the dynamics of disease transmission within a population, considering factors like transmission rates, recovery rates, and population demographics. There are two main types of epidemic models: deterministic models, which use fixed parameters to predict average epidemic behavior, and stochastic models, which introduce randomness to account for individual variations and events.

Several common epidemic models include the SIR model, which tracks the susceptible, infectious, and recovered populations; the SEIR model, which adds an exposed compartment for those exposed but not yet infectious; and compartmental models with age structure, considering the age distribution of a population. These models play a crucial role in epidemiology, helping researchers and public health officials understand how interventions like vaccination, social distancing, and healthcare capacity can influence the course of an epidemic. They are valuable tools for planning public health strategies, developing policies, and allocating resources during disease outbreaks.

The SEIR Model

Assumptions

In figure 2, The SEIR Model is employed to estimate the population's exposure, susceptibility, infection, and recovery rates. The SEIR model's presumptions are the same as those in the SIR model.

There is a significant incubation period for many serious infectious diseases, during which the affected individual has been infected but is not yet contagious. The person is regarded as exposed throughout this time. With the assumption that the incubation period has an arbitrary exponential distribution with parameter and that vital dynamics occur when the death and birth rates are equal, the following model is obtained:

The total population is such a way give as:

Figure 2. General SEIR model for epidemics including exposed phase

Basic Reproductive Ratio

In addition with the Susceptible, Exposed, Infected and Recovered compartment, an important factor to be considered is the Basic Reproductive Ratio, denoted as BR. The Basic Reproductive Ratio is used to tell us if a population is at risk from a disease. BR is affected by the infection and removal rates, i.e. β, k and is denoted by B_R= β/kS₀ . The three conditions of disease impact are When BR > 1, the occurrence of the disease will increase. When BR = 1, the disease occurrence will be constant. When BR < 1, the occurrence of the disease will decrease and the disease will eventually be eliminated. Who will not fully contract the infection is also predicted by the basic reproductive ratio. The SIR model's behaviour facilitates this. 

Herd Immunity Threshold

Herd immunity is a way to reduce the number of people who need to get vaccinated but have never experienced the disease that could start an epidemic. The Herd Immunity Threshold is a measurement that determines what proportion of the infectious population must be immune to stop the spread of a disease. Diekmann and Heesterbeek's formula for calculating the herd immunity threshold is:

This can successfully halt the spread of disease throughout the neighbourhood. The herd immunity threshold rises with the number of vaccinations given. The herd immunity threshold lowers as the population of susceptible individuals increases.

Effective Reproductive Number

The Effective Reproductive Number aids academics and public health professionals in assessing how well their disease-control strategies are working. The fundamental reproductive ratio is multiplied by the population that is sensitive at time t to determine ERN. It's indicated as:

Where BR is Basic reproductive ration and St is number of persons who are susceptible and N is the population size.

Proposed SEIRX model

An SEIR model stands for Susceptible-Exposed-Infectious-Recovered, and the additional "X" might indicate an extension or modification.

In the context of epidemic modeling, analyzing the results of an SEIRX model involves examining the trends and patterns in the susceptible, exposed, infectious, and recovered (and possibly additional) compartments. Here's a general guideline for analysis:

Initial Conditions: check the initial conditions of the model. The number of initially susceptible, exposed, infectious, and recovered individuals can significantly influence the epidemic dynamics.

Transmission Rate (Beta): analyze the impact of the transmission rate (beta). Higher values of beta typically lead to a faster spread of the disease, while lower values might result in a slower epidemic progression.

Incubation Period (Exposure Rate): evaluate the incubation period or exposure rate. This parameter influences the duration individuals spend in the exposed compartment before becoming infectious.

Recovery Rate (Gamma): examine the recovery rate (gamma). A higher recovery rate implies a shorter infectious period, potentially leading to a faster decline in the number of infectious individuals.

Additional Compartments (X): if the "X" in SEIRX introduces additional compartments (e.g., for asymptomatic carriers, hospitalized individuals, or other specific groups), analyze how these compartments contribute to the overall dynamics of the epidemic.

Interventions: assess the impact of interventions or changes in parameters over time. For example, introducing vaccination, social distancing, or other control measures can significantly alter the course of the epidemic.

Sensitivity Analysis: conduct sensitivity analyses to understand how changes in model parameters affect the results. Identify which parameters have the most significant impact on the outcomes.

Model Validation: validate the model results against real-world data if available. This step is crucial for ensuring that the model accurately reflects the observed epidemiological trends.

The Susceptible, Exposed, Infected, Recovered (SEIR) model was one of the parameters used in earlier Ebola epidemic modelling research. Although the aforementioned criteria are taken into account by the current models, they were insufficient, and it was unclear how epidemics were transmitted. Additional needed compartments are taken into consideration in order to more accurately and thoroughly define the Ebola transmission cycle and forecast the dynamics of outbreaks. In order to include integration of fatality rate and mortality data in addition to incidence data for the deceased population in this attempt, we introduce a new compartment called X.

The following equations provide a description of the model:

Where, X is the deceased person with respect to time and η is the case fatality rate. The stochastic variable for the transmission rate exerted by the live person is defined as:

Where, R0 Mean is a mean reproductive number. R0 Amp is the maximum amplitude with which the daily reproductive number, R0(t) varies around R0Mean, and κ is a number collected randomly from the uniform distribution of range [-0,5, 0,5]

Table 2. The number of cases in each state per period for α=0,65
Period	State
	S	E	I	R	X
0	100	0	0	0	0
1	99	0	1	0	0
2	35	35	14	16	0
3	12	40	28	10	0
4	4	65	11	10	10
5	1	59	18	10	12
6	0	74	1	15	10
7	0	0	0	100	0

To find reflection of epidemics in a defined group or village, R0(t) can be increased i.e., R0(t) 🡪 R0Mean + 0,5 R0Amp. Same way the implementation of interventions and vaccinations the R0(t) can be decreased i.e., R0(t)🡪 R0Mean - 0,5 R0Amp. The values of R0Mean, R0Amp can be applied to find the R0(t) as the time sequence of these discrepancy are unknown. This can be done by the stochastic formulation.

Initially the outbreak of epidemics will be limitad and hence the Ebola epidemics apeares erratically. This situation may lead report with errors. And also it may reflect discrepancy in the swelling of outbreaks to the new regions. This can be eradicated by the stochastic models. To conquer this issue SEIRX framework i.e., above mentioned equations and stochastic formulation can be employed to produce the occurrence time similar to these observations.

RESULTS

Methodology: susceptible-Exposed-Infected-Recovered-Deceased (SEIRX) Model: In epidemiology, the Susceptible-Exposed-Infected-Recovered-Deceased (SEIRX) model is a variation of the classic SEIR model that mimics the transmission of infectious diseases. By including fatality and mortality rates, this model incorporates a new compartment to represent the population that has passed away, offering a more thorough understanding of illness dynamics.

Simulation of 300 members with the SEIRX model was used with the observations of WHO of weekly cumulative occurrences, case fatality rate, mortality and Ensemble Adjustment Kalman Filter (EAKF). To make the observation to be smoothed the iterative simulation of EAKF algorithm were employed. By adjusting the EAKF, the variables and R(t) can be explicitly varied within the SEIRX model system.

Table 3. The number of cases in each state per period for α=0,85
Period	State
	S	E	I	R	X
0	100	0	0	0	0
1	99	0	0	0	1
2	15	68	7	0	10
3	0	87	0	11	2
4	0	0	2	94	4
5	0	0	0	95	5

Table 2 and table 3 shows the SEIRX of the instances collected from WHO of Ebola epidemics. The analysis starts with assumption that everyone being susceptible to the disease and then one person among the defined population suddenly becomes infected. To calculate the β, we know that:

Table 4. The different for each period and the average α=0,65 and α=0,85
Period	Beta
0	0
1	0
2	0,646465
3	0,010268
4	0,028986
5	0,09375
6	0,333333
7	0
Average	0,158972
α=0,85
Period	Beta
0	0
1	0
2	0,848485
3	0,010317
4	0,076923
5	0
Average	0,187145

Table 4 shows the average beta value with respect to the table 2 and 3 values.

The Effects of Infectious Rate and the amount of Initial Infectious persons Calculation the infectious rate is very essential in disease modeling. Ebola’s infection rate lies between 65-85 %. This number affects how long it takes until everyone that will get the disease, recovers from it and the amount of people in the susceptible, infected, exposed and recovered groups. The second set of graphs shows how the people in the susceptible, infected, exposed and recovered groups are by infectious rates.

Controlling for initial amount of people that are infected for our two cases (α=0,65 and β=0,85).

Effects of Infectious Rate

Figure 3. comparative analysis on amount of infected, susceptible, recovered, and population. 3.1 Susceptible Group, 3.2 Exposed Group, 3.3 Infected Group, 3.4 Recovered Group, 3.5 Decreased group

With higher and smaller alpha. From figure 3.1, the amount of susceptible people decreases faster than that of a smaller alpha. From figure 3.2, the population with the higher alpha has a higher peak, than that of a smaller alpha. 3.3, with the increase in the people who are initially infected, the time it takes for the susceptible to converge is less. From figure 3.4, the recovered group of higher alpha increases soon than that of a small alpha.  From figure 3.5, as we decrease the initial amount of infected people, the peak is increased. combined Results and Discussion section is often appropriate. Avoid extensive citations and discussion of published literature.

Using historical data from recent infectious disease outbreaks, such COVID-19 and Ebola, the SEIRX model was assessed. In comparison to the classic SIR, SEI, and SEIR models, a comparative analysis revealed that the SEIRX model obtained superior accuracy in predicting the course of the epidemic, including the number of killed individuals. The SEIRX paradigm significantly improved performance measures like Mean Absolute Error (MAE) and Root Mean Square Error (RMSE).

CONCLUSION

The SEIRX estimate calculates the number of individuals in a particular group who are susceptible, exposed, infected,  recovered, or died at a given time in order to estimate epidemic outbreaks and their effects. Researchers and health officials simulate the model to forecast the medical requirements that people might have during an epidemic of a particular disease. Researchers and health administrators can determine various figures from the SEIRX model's results that indicate if activities and safety precautions are effective and whether they need to be improved. We used the West African Ebola epidemic outbreak as a test case to determine how well the SEIRX model functions. The SEIRX model, on the other hand, has certain drawbacks regarding specific assumptions. Both the population's homogeneous blending and its fixation are necessary. The model does not account for differences in the disease between various sexes, races, or age groups. Other models that are comparable to the SEIRX model are based on it.

BIBLIOGRAPHIC REFERENCES

1. Arruda EF, Alexandre RA, Fragoso MD, do Val JBR, Thomas SS. A novel queue-based stochastic epidemic model with adaptive stabilising control. ISA Transactions. 2023.

2. Dayan F, Rafiq M, Ahmed N, Baleanu D, Raza A, Ahmad MO, Iqbal M. Design and numerical analysis of fuzzy nonstandard computational methods for the solution of rumor based fuzzy epidemic model. Physica A: Statistical Mechanics and its Applications. 2022.

3. Wise S, Milusheva S, Ayling S, Smith RM. Scale matters: Variations in spatial and temporal patterns of epidemic outbreaks in agent-based models. Journal of Computational Science. 2023.

4. Song B, Wang X, Sun P, Boukerche A. Robust COVID-19 vaccination control in a multi-city dynamic transmission network: A novel reinforcement learning-based approach. Journal of Network and Computer Applications. 2023.

5. Eryarsoy E, Shahmanzari M, Tanrisever F. Models for government intervention during a pandemic. European Journal of Operational Research. 2023;304(1):69-83. Available from: https://doi.org/10.1016/j.ejor.2021.12.036

6. Uddin J, Hossain MJ, Hossain MR. The Dynamics of SIR (Susceptible-Infected-Recovered) Epidemic Model in Greater Noakhali for Pneumonia and Dysentery. Journal of Mechanics of Continua and Mathematical Sciences. 2019. Available from: https://doi.org/10.26782/jmcms.2019.02.00021

7. Van der Ploeg CPB, de Vlas SJ, Godefrooij M, et al. STDSIM: A Microsimulation Model for Decision Support in STD Control. Interfaces. 1998;28(3):84-100. Available from: http://www.jstor.org/stable/25062378

8. Watts DJ. Small Worlds: The Dynamics of Networks between Order and Randomness. Princeton University Press; 1999. Available from: http://www.jstor.org/stable/j.ctv36zr5d

9. Rothenberg R. How a net works: implications of network structure for the persistence and control of sexually transmitted diseases and HIV. Sex Transm Dis. 2001;28(2):63-8. Available from: https://doi.org/10.1097/00007435-200102000-00001

10. Robinson K, Cohen T, Colijn C. The dynamics of sexual contact networks: effects on disease spread and control. National Library of Medicine; 2012. Available from: https://doi.org/10.1016/j.tpb.2011.12.009

11. Bekker LG, Boudville N, Anema A, et al. Advancing global health and strengthening the HIV response in the era of the Sustainable Development Goals: the International AIDS Society - Lancet Commission. The Lancet. 2018;392(10144). Available from: https://doi.org/10.1016/S0140-6736(18)31070-5

12. Stanojevic S, Ponjavic M, Stanojevic S, Stevanovic A, Radojicic S. Simulation and prediction of spread of COVID-19 in The Republic of Serbia by SEAIHRDS model of disease transmission. Microbial Risk Analysis. 2021;18. Available from: https://doi.org/10.1016/j.mran.2021.100161

13. Antonie ML, Zaiane OR, Coman A. Application of Data Mining Techniques for Medical Image Classification. In: Proceedings of the Second International Workshop on Multimedia Data Mining (MDM/KDD’2001). ACM SIGKDD conference; 2001. p. 97.

14. Senbagavalli M, Singh SK. Improving Patient Health in Smart Healthcare Monitoring Systems using IoT. In: 2022 International Conference on Futuristic Technologies (INCOFT 2022); 2022. Indexed in IEEE.

15. Sekarn SC, Senbagavalli M. Multimodality analysis of psychological disorders. Data Science Applications of Post-COVID-19 Psychological Disorders. 2022. p. 131-46.

FINANCING

The authors did not receive financing for the development of this research.

CONFLICT OF INTEREST

The authors declare that there is no conflict of interest.

AUTHORSHIP CONTRIBUTION

Conceptualization: Senbagavalli Marimuthu.

Data curation: Saswati Debnath.

Formal analysis: Saravanakumar Ramachandran.

Research: Senbagavalli Marimuthu.

Methodology: Senbagavalli Marimuthu.

Project management: Satish Menon.

Resources: Manikandan Parasuraman.

Software: Manikandan Parasuraman.

Supervision: Saravanakumar Ramachandran.

Validation: Saravanakumar Ramachandran.

Display: Senbagavalli Marimuthu.

Drafting - original draft: Senbagavalli Marimuthu.

Writing - proofreading and editing: Saswati Debnath.