doi: 10.56294/sctconf2024.1019

Category: STEM (Science, Technology, Engineering and Mathematics)

ORIGINAL

Optimized design and research of direct-drive permanent magnet synchronous motor for hydra pulper

Diseño optimizado y la investigación del imán permanente de acción-directo Motor sincrónico para hydra pulper

Fengmei Shen¹ *, Celso Bation Co¹ *, Rowell M. Hernandez¹ *

¹College of Engineering, Batangas State University. The National Engineering University, Alangilan Campus. Batangas City 4200, Philippines.

Cite as: Shen F, Bation Co C, Hernandez RM, Co CB. Optimized design and research of direct-drive permanent magnet synchronous motor for hydra pulper. Salud, Ciencia y Tecnología - Serie de Conferencias. 2024; 3:.1019. https://doi.org/10.56294/sctconf2024.1019

Submitted: 05-02-2024                   Revised: 10-05-2024                   Accepted: 19-08-2024                 Published: 20-08-2024

Editor: Dr. William Castillo-González

ABSTRACT

This paper presents the design of a direct drive permanent magnet synchronous motor specifically tailored for the transmission of a hydra pulper, boasting a rated power of 350 kW and a rated speed of 230r/min. A finite element model of the direct drive permanent magnet synchronous motor is established to comprehensively analyze various performance parameters, encompassing magnetic characteristics, magnetic circuitry, reverse electromotive force, and more. Employing the coercive force method in conjunction with the magnetic density method, the demagnetization propensity of the permanent magnet under extreme operating conditions is evaluated and analyzed, facilitating the rapid identification of boundary size conditions for the permanent magnet and thereby mitigating overall motor costs. Furthermore, a genetic algorithm is employed to optimize the structural parameters of the direct-drive permanent magnet synchronous motor, enhancing comprehensive performance parameters such as power, efficiency, power factor, torque ripple, among others, while ensuring the motor remains demagnetization free.

Keywords: Hydra Pulper; Direct Drive Permanent Magnet Synchronous Motor; Finite Element Analysis; Genetic Algorithm.

RESUMEN

Este trabajo presenta el diseño de un motor sincrónico de imanes permanentes de accionamiento directo especialmente diseñado para la transmisión de un pulper hydra, con una potencia nominal de 350 kW y una velocidad nominal de 230r/min. Un modelo de elementos finitos del motor sincrónico de imán permanente de acciondirecto se establece para analizar exhaustivamente varios parámetros de rendimiento, que abarcan características magnéticas, circuitos magnéticos, fuerza electromotriz inversa, y más. Empleando el método de la fuerza coercien conjunto con el método de la densidad magnética, se evalúa y analiza la propensión a la desmagnetización del imán permanente bajo condiciones operativas extremas, lo que facilita la rápida identificación de las condiciones de tamaño de contorno para el imán permanente y, por lo tanto, mitigar los costos generales del motor. Además, se emplea un algoritmo genético para optimizar los parámetros estructurales del motor sincrónico de imán permanente de acciondirecto, mejorando parámetros de rendimiento completos como potencia, eficiencia, factor de potencia, onduldel par, entre otros, mientras se garantiza que el motor permanece libre de desmagnetización.

Palabras clave: Hydra Pulper; Motor Sincrónico de Imán Permanente de Accionamiento Directo; Análisis de Elementos Finitos; Algoritmo Genético.

INTRODUCTION

In recent years, scholars have extensively explored the starting performance, synchronization capability, and steady state performance of permanent magnet synchronous motors (PMSMs). Firstly, improved traction synchronization criteria and dynamic simulation models are proposed to analyze the starting process of the motor, improving synchronization capability through parameter adjustments such as excitation inductance and permanent magnet strength, although this may sacrifice starting torque. In addition, through structural optimization such as the improvement of rotor squirrel cage bars and the use of ferrite assisted synchronous reluctance motor design, the reluctance torque and operating efficiency of the motor can be enhanced.^{(1,2,3,4,5,6,7)} The study also explored ways to enhance traction synchronization capability by reducing the number of series turns per phase, increasing rotor resistance, and adjusting other electromagnetic parameters.^(8,9,10) Finally, genetic algorithms and NSGA-II optimization strategies were applied to optimize the torque ripple, cogging torque, and improve power density and efficiency of motors.^{(11,12,13,14)} These studies indicate that by comprehensively applying structural design, parameter optimization, and advanced algorithms, the overall performance of permanent magnet synchronous motors can be effectively improved.

This article addresses the deficiencies found in prior research concerning the demagnetization of permanent magnets, with a primary focus on investigating the demagnetization mechanism, analyzing demagnetization characteristics, and optimizing structural parameters to mitigate demagnetization risks. The ultimate aim is to enhance the performance and reliability of permanent magnet synchronous motors, particularly targeting the design requirements for a 350 kW, 230 r/min permanent magnet synchronous motor. The study encompasses an examination of demagnetization curves and mechanisms, the establishment of a two dimensional simulation model, an analysis of the correlation between structural configurations and demagnetization tendencies, and the utilization of genetic algorithms for motor optimization, specifically targeting torque and efficiency enhancements.

Finite element modeling based on maxwell software

Analysis of demagnetization mechanism

The magnetization characteristics of permanent magnet materials can be described by hysteresis loops, as shown in figure 1, which shows the relationship between magnetic induction intensity B and magnetic field intensity H. The hysteresis loop is formed at the saturation magnetic field strength Hs, and its area size reflects the stability of the material's magnetic properties. The demagnetization curve of the permanent magnet material is located in the second quadrant, showing the reverse relationship betweenand, indicating that the permanent magnet serves as a magnetic source. The magnetic properties are represented by residual magnetism Br and coercive force Hc, and the larger these two parameters, the better the magnetic properties of the permanent magnet.

Figure 1. Magnetic hysteresis loop

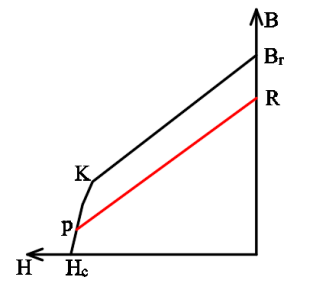
Figure 2. The demagnetization curve of the permanent magnet material

Permanent magnet materials typically exhibit a straight demagnetization curve, indicating that they do not undergo spontaneous demagnetization. As shown in figure 2, when the strength of the reverse magnetic field exceeds a certain threshold, the magnetic density will sharply decrease at the inflection point, leading to magnetic energy loss. To ensure the long term stable operation of permanent magnet synchronous motors, it is necessary to maintain the chemical, time, magnetic, and thermal stability of the permanent magnet. Thermal stability describes the impact of temperature on magnetic performance, divided into recoverable and irreversible losses, the former measured by temperature coefficient. The main demagnetization methods considered in the built-in permanent magnet synchronous motor used in hydraulic pulp crusher are high temperature demagnetization and AC demagnetization. Demagnetization can lead to a decrease in motor performance, an increase in current and temperature, forming a vicious cycle that further exacerbates magnetic energy loss. Therefore, research on demagnetization of these motors is very important.

Main parameters and modeling of the motor

This study focuses on a 350kW built in permanent magnet synchronous motor, as shown in table 1. The motor parameters were preliminarily designed and a model was constructed in Maxwell finite element simulation software. The motor has 108 stator slots and a 24 pole "V" type built-in rotor magnetic circuit, and the stator winding is a three phase double layer structure. After preliminary optimization, a two dimensional simulation model of the motor was obtained as shown in figure 3.

Figure 3. A 2-dimensional simulation model of a built-in PMSM

Table 1. Main parameters of the built-in permanent magnet synchronous motor
Parameters	value	Parameters	value
Outer diameter of stator D s out/mm	1 600	Inner diameter of Stator Ds in / mm	1350
Outer diameter of rotor Dr out/mm	1 345,6	Inner diameter of Rotor Dr in / mm	1080
Axial length Lef /mm	175	Air gap length is δ / mm	2,2
Permanent magnet thickness TM/mm	13,9	The permanent magnet width is WM / mm	91
number of pole pairs p	12	Stator slot number Q1	108
Rated rotational speed of n / rmin-1	230	Reference power: P / kW	350
Permanent magnet model	N48SH	Silicon steel chip model	B35A300
Number of parallel branches, a	6	Each groove of the conductor NS	13

Calculation of the motor parameters

The calculation formula of the stator winding phase resistance is:

Where p_cu is the resistivity of the copper wire, S_c is the cross sectional area of the stator winding coil, l_c is the average half turn length, and N is the number of series turns per phase.

The resistivity of copper wire changes with temperature, and within a certain temperature range, the resistivity of copper wire is directly proportional to temperature. According to calculations, the resistance values of each phase of the motor stator winding at different temperatures are shown in table 2. When the armature current is small, the temperature of the stator winding is not high, and the resistance value is also small. The copper wire loss generated by the motor is small. However, as the current increases, the temperature also increases, and copper loss will become the main loss of the motor.

Table 2. resistance value per phase of the motor stator winding
Temperature °C	Resistance value/Ω	Temperature °C	Resistance value/Ω
0	0,009794	60	0,012067
10	0,010143	70	0,012592
20	0,010493	75	0,012767
30	0,010843	80	0,012942
40	0,011368	90	0,013291
50	0,011717	100	0,013816

No-load anti-electric potential

The no-load back electromotive force is a key parameter of permanent magnet synchronous motor during no-load operation. It is induced by the fundamental wave magnetic flux of the no-load air gap generated by the permanent magnet of the rotor in the stator winding, which can reflect the working state of the permanent magnet motor and also affect the static and dynamic performance of the permanent magnet motor. The calculation formula is as follows:

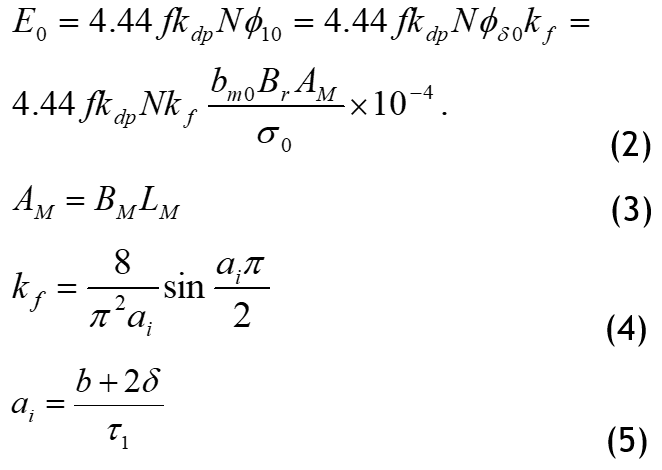
Where K_dp is the winding factor, K_f is the waveform coefficient of the air gap magnetic field; δ is the length of the air gap between the stator and rotor; σ₀ is the no-load leakage magnetic coefficient; b_m0 is the amplitude of the fundamental magnetic flux density of the permanent magnet; A_M provides the magnetic flux area of each pole for the permanent magnet, and the rotor magnetic circuit of the built-in permanent magnet synchronous motor is radial; B_M and L_M are the magnetic pole width and axial length of the permanent magnet, respectively; a_i is the pole arc coefficient; b is the arc length of the extreme boot; t_i is the stator pole distance.

According to equation (2), it can be seen that is directly proportional to the residual magnetism, When the working temperature of the permanent magnet is different, the residual magnetization of the demagnetive curve is not the same. The higher the temperature, the smaller the residual magnetism is. From formula (3-5) and finite element analysis, the effective value of the built-in permanent magnet synchronous motor is shown in table 3.

Table 3. no-load back emf values at different temperature
Temperature °C	Permanent magnet flux chain φf/Wb
20	3,3107
50	3,2273
80	3,1439
100	3,0884
120	3,0328
150	2,9494

Permanent magnet magnetic chain the formula for the magnetic flux chain φf of a permanent magnet is:

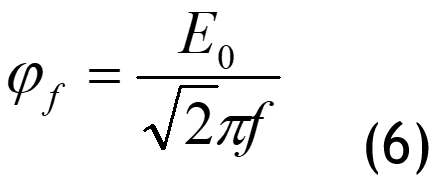
The values of Eo at various temperatures have been obtained in table 2, according to formula (6),the frequency remains constant and the magnetic flux of the permanent is directly proportional to it. The values of the magnetic chain of the permanent magnet at different temperatures are shown in table 4:

Table 4. no-load back emf values at different temperature
Temperature °C	Permanent Magnet Flux Chain φf/Wo
20	3,3107
50	3,2273
80	3,1439
100	3,0884
120	3,0328
150	2,9494

When conducting finite element analysis using Maxwell software, using current excitation results in a short starting time and the motor can reach a stable operating state faster .Therefore, the sinusoidal current excitation with amplitude 341A is adopted, the twelfth model is adopted, and the step length is set as 0,00043478ns, and the basic torque effective average torque of the built-in permanent magnet synchronous motor is 14,622kN·m. As shown in figure 4, the torque pulse is 2,97 %; as shown in figure 5, the no-load reverse EMF is about 672,3V; as shown in figure 6, the carrier voltage waveform is 695,67V. The value of FFT analysis of the carrier voltage waveform is shown in figure 7. According to figure 7, the proportion of available harmonics is 3,18 %, which exceeds 3 %. The motor parameters are only initially optimized, so the proportion of torque pulsation and harmonic is too large, and further optimization design will be carried out, so that the optimized motor can be reduced under the premise of meeting the demagnetization.

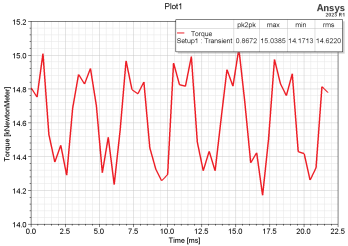
Figure 4. Electromagnetic torque of interior permanent magnet synchronous motor

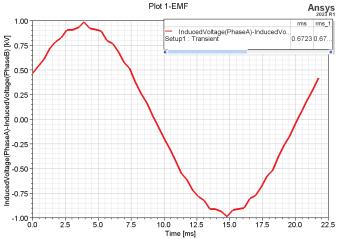
Figure 5. No-load reverse EMF

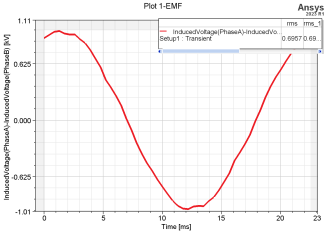
Figure 6. Load input voltage waveform

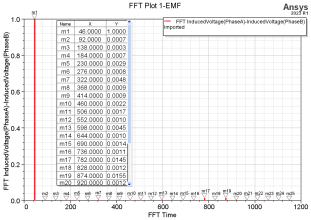
Figure 7. Harmonic analysis of no-load in FFT

Effect of different magnetic tile sizes on demagnetization

In this paper, the permanent magnet material of the built-in permanent magnet synchronous motor is NdfeB N48SH. The demagagnetic curve of the permanent magnet working at different temperatures is shown in igure 8, and the highest operating temperature is 150℃. When the working temperature of the permanent magnet is not higher than 100℃, the demagagnetic curve of N48SH permanent magnet material is basically a straight line. After the demagnetic magnetic field is evacuated, the permanent magnet will not produce magnetic energy loss. When the working temperature of the permanent magnet is higher than 100℃, the demagagnetic curve obviously has an inflection point. If the strength of the demagnetic magnetic field exceeds the strength of the inflection point, the magnetic density of the permanent magnet will drop sharply. After the withdrawal of the demagnetic magnetic field, the remaining magnetic field can not return to the original value, resulting in irreversible demagnetization. The magnetic density value corresponding to the inflection point of the N48SH permanent magnet materials at 120℃, 130℃, and 150℃ demagnetization curves is 0,22T, 0,31T, 0,5T, respectively.

In Maxwell finite element software, the motor was parameterized, and the influence of magnetic tile shape on the demagnetization of permanent magnets was initially explored. The coercive force method was used for preliminary analysis to determine the effect of magnetic tile shape on demagnetization. Subsequently, the magnetic density method was applied to accurately obtain the boundary value of the magnetic tile size that prevents demagnetization of the permanent magnet under specific conditions.

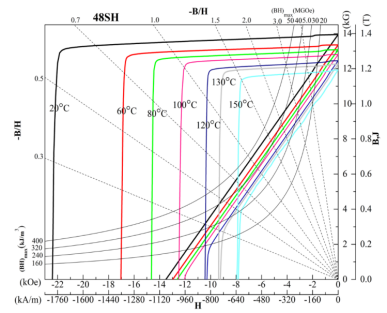
Figure 8. NdFeB N48SH demagnetization curve

Coercivity method: this article employs Maxwell to scan the parameters of magnetic tile thickness (TM) and magnetic tile width (WM) to assess the influence of magnetic tile length and thickness on demagnetization and to identify patterns. Applying identical demagnetization conditions to motors featuring different thicknesses of magnetic tiles allows for the determination of the coercive force magnitude generated by the motor under varying magnetic tile thicknesses. As indicated by the abscissa of the demagnetization curve in figure 9, it becomes evident that when the coercive force value exceeds or approaches 620kA/m, the motor will undergo irreversible demagnetization. The 8mm thick magnetic steel is closest to this threshold and is thus more susceptible to demagnetization. Based on figure 10, it is apparent that, with the same length of magnetic tile, thicker tiles exhibit better anti-demagnetization capabilities. Similarly, with identical magnetic tile thickness, narrower tiles demonstrate stronger anti-demagnetization abilities.

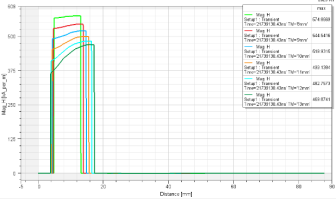
Figure 9. WM=97,5mm, TM=8-13mm

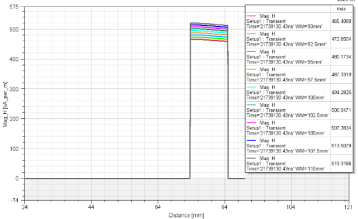
Figure 10. WM=90-110mm, TM=11mm

Magnetic compaction method: the prerequisite for analyzing the impact of different sizes on demagnetization is to ensure the performance of the motor, including output power, motor efficiency, power factor, and other parameters. As depicted in figure 11, under constant current conditions, the motor's output power increases with the growth of WM and TM. Consequently, as the size of the magnetic tile increases, both the output power and efficiency of the motor improve. As illustrated in figure 12, under constant current conditions, the motor's efficiency gradually increases with the rise of WM and TM. Initially, the change in efficiency is relatively substantial, followed by a smaller change amplitude. Demagnetization analysis for the magnetic tile sizes outlined in table 5 enables the generation of a Magnetic Cloud Map, as depicted in figure 13.

Table 5. Motor performance simulation results
TM (mm)	WM (mm)	Input power (kW)	Output power (kW)	Power factor	Productiveness
9	110	371,2079	354,361	0,961	97,659 %
10	102,5	367,215	350,768	0,959	97,656 %
11	97,5	366,5603	349,982	0,960	97,657 %
12	95	371,0144	354,557	0,964	97,675 %

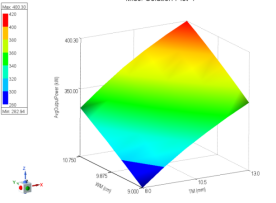
Figure 11. The relationship between magnetic tile size and motor output power

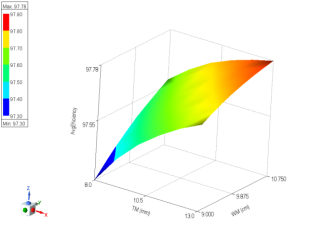
Figure 12. The relationship between magnetic tile size and motor efficiency

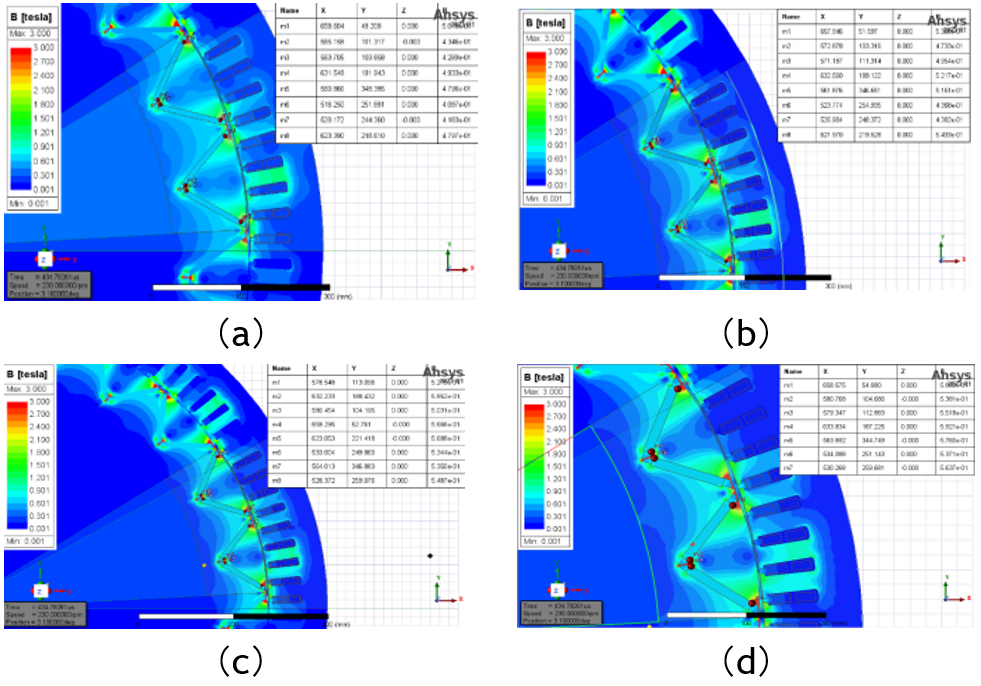
Figure 13. Magnetic cloud map of different magnetic tile sizes:（a）TM=9mm，WM=110mm;（b）TM=10mm，WM=102,5mm;（c）TM=11mm，WM=110mm;（d）TM=12mm，WM=95mm.

Table 6. to meet the motor performance of permanent magnet size parameters
TM (mm)	WM (mm)	Maximum magnetic density	Minimum magnetic density value	Whether the 150℃ is satisfied	Whether the 130℃ is satisfied
9	110	0,501	0,408	dissatisfaction	satisfied
10	102,5	0,543	0,436	dissatisfaction	satisfied
11	97,5	0,568	0,503	Just meet	satisfied
12	95	0,592	0,538	satisfied	satisfied

According to figure 13.we can summarized in table 6, It can be seen from the table 6 that both the demagnetization and motor performance are met, and the optimal cost of the magnetic tile size is 11*97,5mm.

The influence of the different tension angles of the permanent magnets on the demagnetization

Figure 14 illustrates the parameters of the built-in V-type permanent magnet motor rotor. The tension angle (A) of the magnetic tile can only be altered by adjusting Mag_O2. With TM = 11mm and WM = 97,5mm kept constant, demagnetization density is solely compared between the smallest and maximum tension angles, i.e., Mag_O2 = 20 mm and Mag_O2 = 36 mm,as shown in the figure 15, From figure 15 can got the result in table 7. When the magnetic tile size remains unchanged, the influence of the magnetic tile angle on demagnetization can be disregarded.

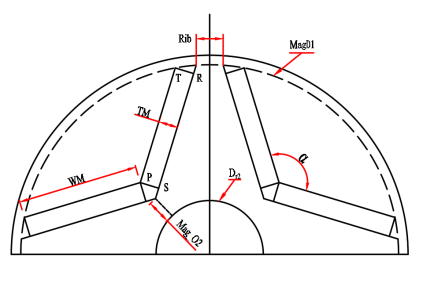
Figure 14. Built-in V-type permanent magnet motor rotor reference

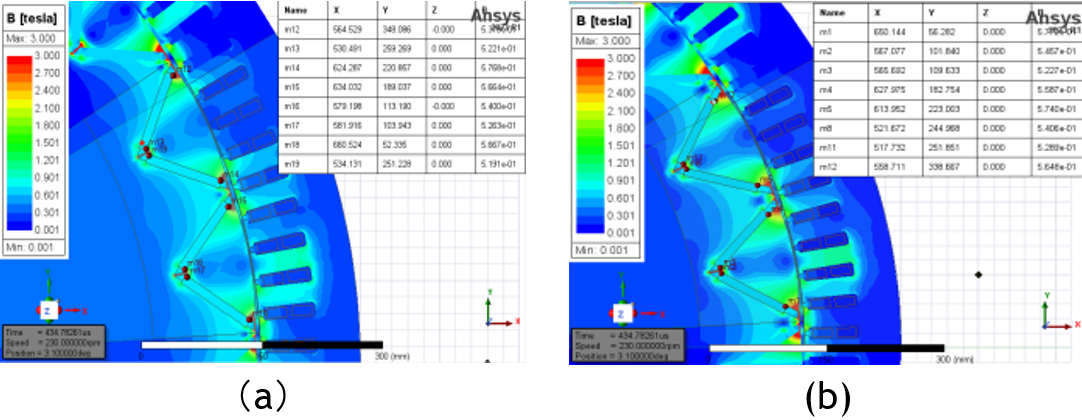
Figure 15. Magnetic graph of the maximum and minimum angles: (a) Mag _O2 = 36 mm; (b) Mag _O2 = 20 mm

Table 7. magnetic density value at the limit tension angle of the magnetic tile
Mag_O2:mm	Maximum magnetic density	Minimum magnetic density value
20	0,577	0,522
36	0,576	0,519

Establishment of the optimization mode

Optimization parameters of the motor

Pole-arc coefficient: as depicted in figure 16, the polar-arc coefficient denotes the radian proportion of the permanent magnet material on the rotor in the permanent magnet synchronous motor, influencing the distribution of the air gap magnetic field. The pole-arc coefficient is closely associated with tooth groove torque. An appropriately designed coefficient can mitigate waveform distortion, enhance torque pulse performance, and diminish the leakage energy of magnetic force lines in the core magnetic circuit, thereby augmenting the motor's output performance.

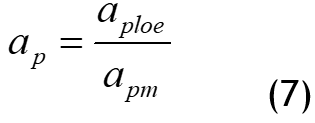
In formula: a_ploe, a_pm are the center angle corresponding to the arc length of the pole distance, a_p is the pole-arc coefficient.

By optimizing the Pole-arc coefficient, the interaction force between the magnetic steel and the teeth in permanent magnet motors can be significantly reduced, thereby reducing torque ripple, enhancing motor rotational stability, reducing mechanical wear, and extending service life. Meanwhile, an appropriate pole arc coefficient can also improve the efficiency of the motor. In the simulation model, the polar arc coefficient can be achieved by adjusting the parameters Mag_O2 and Rib. Figure 14 clearly shows the significance represented by these two parameters.

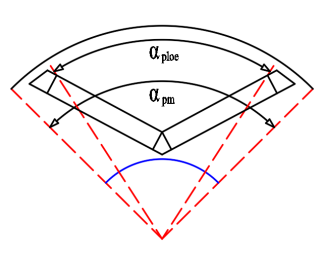
Figure 16. Schematic representation of the pole-arc coefficient

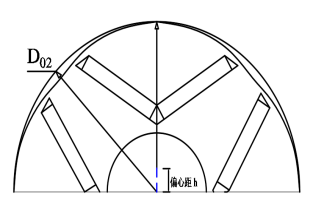
Figure 17. Schematic representation of the eccentricity distance

Eccentricity: by employing an eccentric design featuring unequal air gaps, the tooth slot torque can be further mitigated by altering the magnetic resistance of the air gap and shaping the magnetic field. Simultaneously, the air gap ensures a low distortion rate in the motor's magnetic density waveform, thereby diminishing torque ripple resulting from distortion. Consequently, torque pulsation can be reduced on both fronts, as illustrated in figure 17.

Angle of lead: the leading angle has a great impact on the iron loss of the motor stator, so it is also included in the optimization target simultaneously.

Determination of the motor optimization objective and objective function

Selection of optimized variables: In motor optimization design, all structural parameters can be considered as design variables. In fact, the parameters with great influence on the motor optimization targets are usually selected. Considering the important influence of air gap magnetic field on torque, through theoretical analysis and extensive simulation found that the position of the permanent magnet to the axis (Mag_O2)O2, adjacent two spacing Rib, the rotor eccentric h, current lead Fw four variables have a significant influence on the torque and slot torque of the motor, so these variables are selected as optimization design variables, optimized under the premise that the stator outer diameter and air gap length is constant.

Table 8. Initial values and variation ranges of the main optimized parameters
Parameter	starter	excursion
Permanent magnet to the axis position O2 / mm	18	1-35
Distance to Rib / mm of adjacent two-level spacing	12,5	5-20
The eccentric distance h / mm	200	50-350
Current lead angle Fw / deg	15	0-30

Determination of the objective function: combined with the application occasions, the following four motor parameters are the focus of the design.1, the efficiency of the motor; 2, output power; 3, power factor PF; 4, torque ripple Tr. The optimization targets were extracted from the 4 parameters. In order to simplify the objective function, the efficiency and output power of the motor are converted into torque T. On the premise of constant current, The greater the torque, the greater the motor efficiency and output power. The objective function is as follows:

Where, w1, w2, w3 are the weight coefficient, meet w1 + w2 + w3 = 1, the optimization takes w1=0,6, w2=0,2, w3=0,2, T is the torque, negative sign is the maximum value; T0, PF0, Tr0 set the base value to eliminate the order of magnitude difference between the two targets.

Settings of the constraints: in motor optimization design, constraints define the feasible domain within the search range, ensuring that the algorithm can iteratively converge towards the optimal solution. The optimization process entails incorporating nonlinear or linear programming constraints on the variable boundaries and potentially on the motor's output performance. When prioritizing the output torque under rated conditions as the optimization objective, it becomes imperative to consider potential high magnetic loads within the population. Hence, performance parameters such as magnetic density B_t and B_j in the tooth yoke are selected as constraints.

According to the characteristics of GA as unconstrained optimization, the punishment function is introduced to further improve the objective function, select the appropriate punishment intensity, and speed up the optimization process, but the punishment intensity should be carefully dealt with. The strict punishment function will make the algorithm unable to obtain viable individuals. Using the penalty mechanism, the constraint optimization in motor optimization can be transformed into the unconstrained optimization problem implemented by GA.

The penalty function is constructed as follows: The penalty function is constructed as follows:

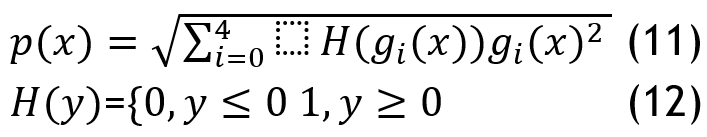
Where H_(Y) is the step function, the augmented objective function is:

Optimization results: the parameter comparison table optimized by genetic algorithm is shown in table 9 below. Furthermore, we rounded the optimized data.

Table 9. The result of each variable before and after optimization
Parameter	Un-optimization	Post-optimized
Permanent magnet to the axis position O2	1	35
The distance of the adjacent two-level spacing, Rib	5	20
The rotor eccentricity is h	50	310
Current lead angle Fw	0	15

Comparison between before and after torque pulsation optimization.

Figure 18. Torque pulsation before and after optimization: (a) 6,5384 % before optimization; (b) 1,3695 % after optimization

Through the analysis and calculation of the torque waveform, the optimized torque pulsation is greatly reduced to within 3 % to meet the design requirements.

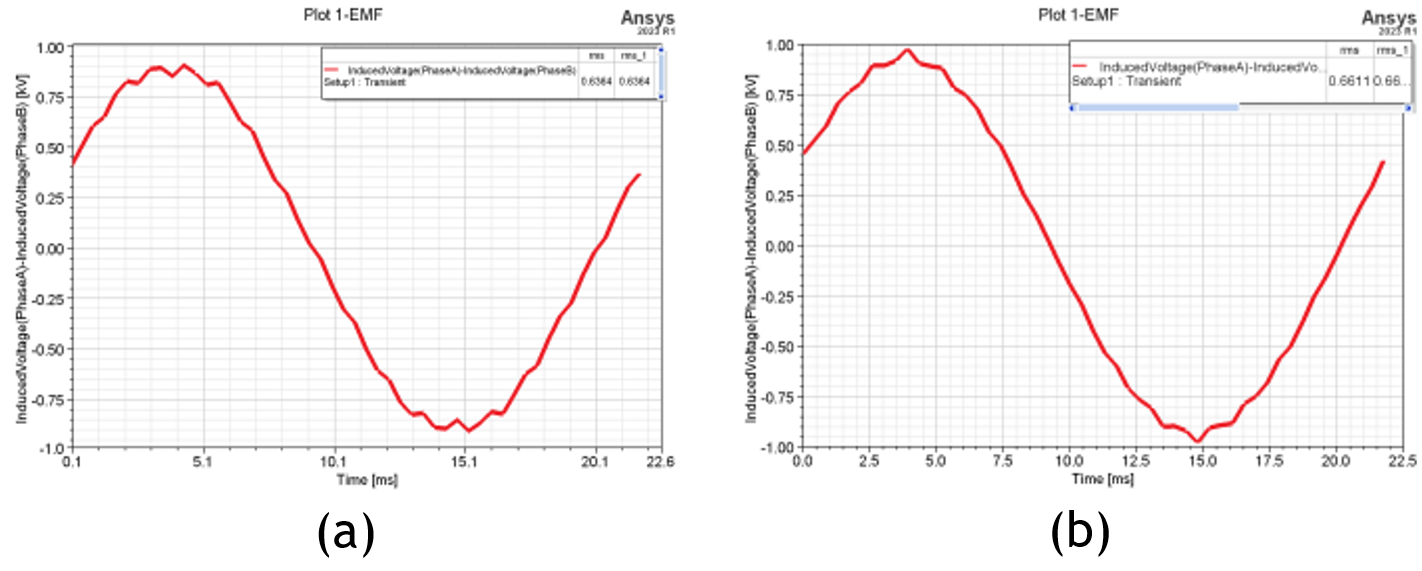
Figure 19. No-load back-EMF waveform before and after optimization: (a)Un-optimization; (b) Post-optimized.

Figure 20. Harmonic contrast of in EMF before and after optimization

Table 10. Harmonic ratio values of the optimized order
Parameter	Un-optimization	Post-optimized
Carrying idler THD	3,36 %	2,25 %

FFT analysis to figure 19 of the optimized no-load back-EMF, we got the result of figure. 20. it shows that the 5 harmonics with 17 harmonics decrease significantly and the 7 harmonics increase slightly, but the total harmonics are less than 3 %, meeting the design requirements, as shown in table 10.

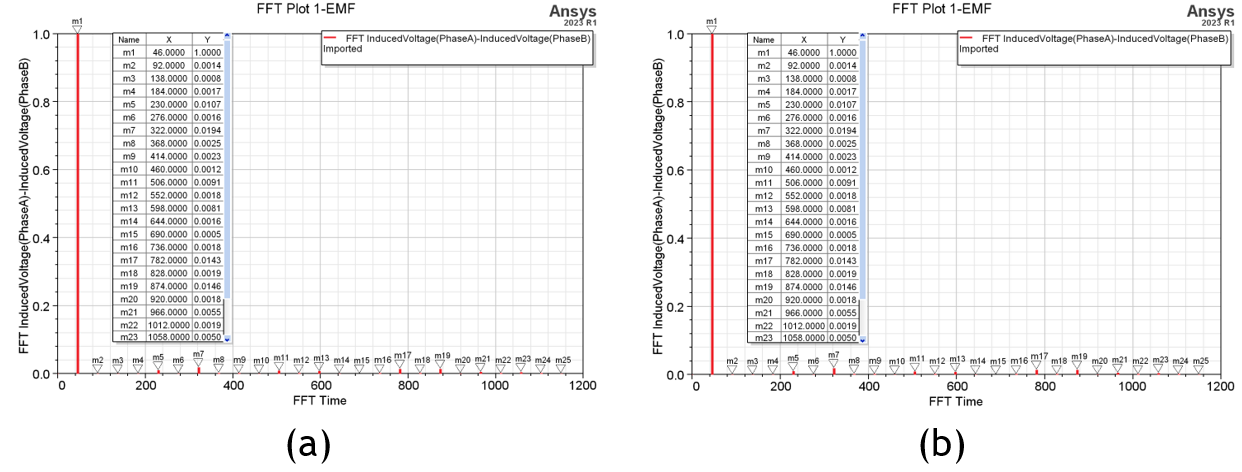
Figure 21. The ratio of full-load harmonics before and after optimization: (a) 3,4083 % Un-optimization; (b) 2,3574 % Post-optimized

Table 11. comparison of motor performance before and after optimization
Parameter	Unoptimization	Postoptimality	Performance improvement ratio	Design requirement
Output Power [kW]	324,05	360,02	11,1 %	≥350
Power Factor [%]	0,82	0,97	17,7 %	≥0,95
Efficiency [%]	96,23	96,68	0,5 %	≥0,95
With the loaded THD [%]	3,4083	2,36	-30,8 %	＜3
Carrying idler THD[%]	3,36	2,25	-33 %	＜3
Torque ripple[%]	6,54	1,37	-79,1 %	＜3

According to the simulation data before and after optimization, the power is increased by 11,1 %, exceeding the designed power by 350KW, the power factor is 97 % higher than the given design value, the proportion of motor harmonics with load and full load is less than 3 %, and the torque pulsation is reduced from the initial 6,54 % to 1,37 %, meeting the design requirements.

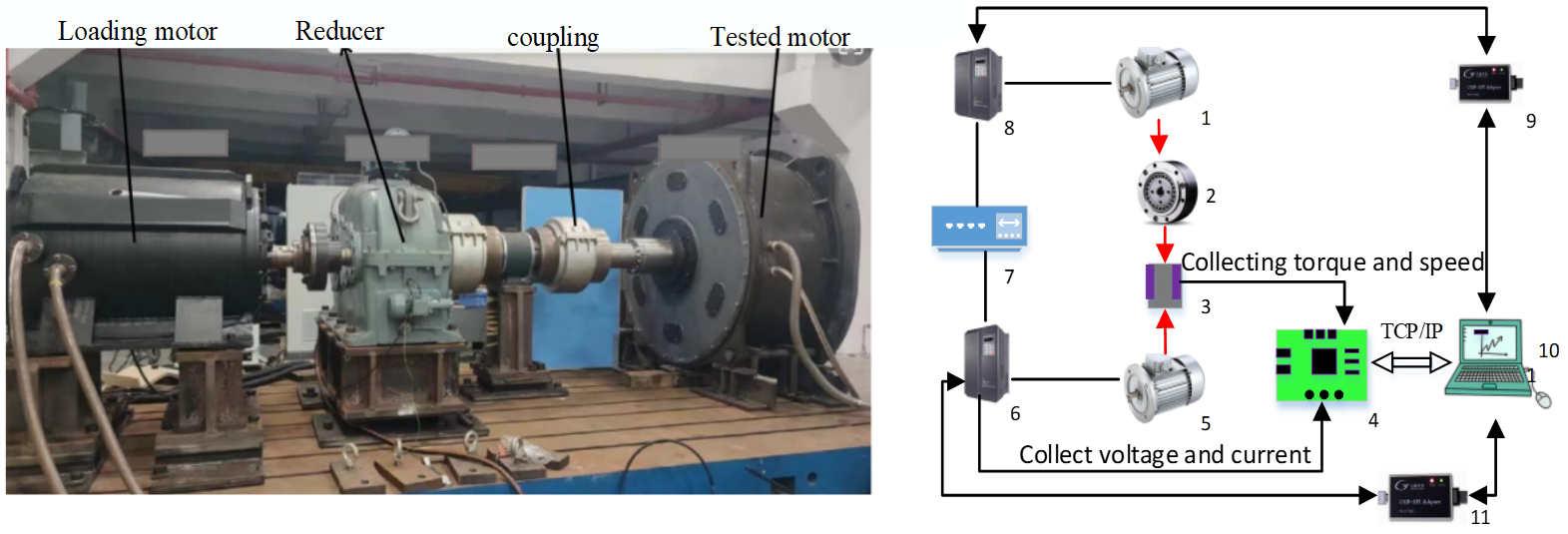
Figure 22. An Experimental test platform

Where: 1-Loading motor; 2-Reducer; 3-torque sensor; 4-Power analyzer; 5-Tesed motor; 6-Motor driver; 7-Three phase sources;8-Motor driver;9-USB to CAN module; 10-Computer;11-USB to CAN module.

Table 12. Actual measurement of various performance parameters of the motor
Speed [N/min]	LineVoltage [V]	Current [A]	InputPower [kW]	OutputPower [kW]	Torque [N·M]	Simulation efficiency of Efficiency
230	633,4	68,2	82,2	74,36	3 087,5	90,5
230	642,0	136,3	155,6	147,39	6 120,0	95,1
230	655,9	204,5	227,4	218,14	9 057,6	96,1
230	662,5	272,7	300,5	289,92	12 038,2	96,5
230	661,6	340,8	373,1	360,86	14 983,6	96,8

Due to the low rotational speed of the current motor, it is High-scale torque, To satisfy the test, The loading motor is a 500kW, Motor at 1500 rpm, Use a 5:1 speed reducer in the middle, Use a torque sensor measuring

50 000N·m, The motor of the final type design, The input power Pin of the motor is calculated by detecting the three-phase input voltage and current of the motor by a power analyzer, Pout = TN / 9550, The test block diagram and test object are shown in figure 22, table 12 shows that the efficiency of the simulation is almost comparable to the measured efficiency, It shows that the simulated model agrees with the reality.

CONCLUSION

 This paper uses the finite element analysis method to analyze the magnetic performance, magnetic chain, reverse electromotive force and other parameters of the permanent magnet, judge the demagnetization by coercivity method and magnetic density method, and optimize the electromagnetic parameters of the motor by genetic algorithm. The main research contents and results of this paper are as follows:

Based on the operational features of the hydraulic slurry mill, the foundational parameters and performance criteria for a direct drive permanent magnet synchronous motor are established. An embedded motor design is chosen, with N48SH as the permanent magnet material, stator winding as the motor winding, and a frequency converter with FVC function as the motor controller. Parameters like stator outer and inner diameters, fracture ratio, and air gap are determined through practical experience. A finite element model for the direct drive permanent magnet synchronous motor is constructed, and the motor's magnet is analyzed using the coercive and magnetic density methods to ascertain the magnet's size while meeting the performance requirements.

The motor parameters are then optimized using a genetic algorithm. The polar arc coefficient, eccentric distance, and advance angle are selected as the optimization variables, with their ranges defined by the model structure. The objective function and weighting coefficient are determined, and to expedite convergence, constraints and penalty functions are incorporated into the genetic algorithm. Following optimization, Fast Fourier Transform (FFT) analysis is performed on the motor's EMF under no-load and full-load conditions, revealing a 30 % reduction in harmonic ratio THD, a 11,1 % increase in motor power, a 79,1 % decrease in torque pulsation, and a reduction in torque pulsation from 6,54 % to 1,37 %. The motor's testing confirms the simulation model and algorithm's validity, aligning with the simulation outcomes.

BIBLIOGRAPHIC REFERENCES

1. F. Mahdavi, A. D. Aliabad, E. Amiri, et al. Dual-pole line start synchronous machine with consequent-magnetic poles[J]. IEEE Transactions on Energy Conversion, 2020, 35(3): 1648-1657.DOI: 10.1109/TEC.2020.2986462

2. M. Lin, D. Li, X. Ren, et al. Line-start vernier permanent magnet machines[J]. IEEE Transactions on Industrial Electronics, 2021, 68(5): 707-3718. DOI: 10.1109/TIE.2020.2982102

3. M. F. Palangar, A. Mahmoudi, S. Kahourzade, et al. Electromagnetic and thermal analysis of a line-start permanent-magnet synchronous motor[C]// Energy Conversion Congress and Exposition (ECCE). Detroit, MI, USA: IEEE, 2020: 502-508. DOI: 10.1109/ECCE44975.2020.9235632

4. Isfahani A H, Vaez-Zadeh S. Line start permanent magnet synchronous motors: challenges and opportunities[J]. Energy, 2009, 34(11): 1755-1763. https://doi.org/10.1016/j.energy.2009.04.022

5. C. G. Heo, H. M. Kim, G. S. Park. Design of rotor bar inclination in squirrel cage induction motor[J]. IEEE Transactions on Magnetics, vol. 53, no. 11, pp. 1-4, Nov. 2017. DOI 10.1109/TMAG.2017.2696977

6. S. Baka, S. Sashidhar, B. G. Fernandes. Design and optimization of a two-pole line-start ferrite assisted synchronous reluctance motor[C]//Proc. XIII Int. Conf. Elect. Mach.. Alexandroupoli, Greece: IEEE, 2018: 131–137.DOI: 10.1109/ICELMACH.2018.8507187

7. S. Baka, S. Sashidhar, B. G. Fernandes. Design of an energy efficient line-start two-pole ferrite assisted synchronous reluctance motor for water pumps[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 961-970. DOI: 10.1109/TEC.2020.3029110

8. Waheed, J. -S. Ro. Analytical modeling for optimal rotor shape to design highly efficient line-start permanent magnet synchronous motor[J]. IEEE Access, 2020, 8: 145672-145686.DOI: 10.1109/ACCESS.2020.3014718

9. M. F. Palangar, A. Mahmoudi, S. Kahourzade, et al. Optimum design of line-start permanent-magnet synchronous motor using mathematical method[C]//Energy Conversion Congress and Exposition (ECCE). Detroit, MI, USA: IEEE, 2020: 2064-2071.DOI: 10.1109/ECCE44975.2020.9236205

10. J. Pecho, W. Hofmann. Analysis of the effects of parameter variations on the start-up characteristics of LSPMSM[C]//Proc. 21st Eur. Conf. Power Electron. Appl.. Genova, Italy: IEEE, 2019: 1–10.DOI: 10.23919/EPE.2019.8914800

11. Mahmood Z, Ikram J, Badar R, et al. Minimization of Torque Ripples in Multi-Stack Slotted Stator AxialFlux Synchronous Machine by Modifying Magnet Shape[J]. Mathematics, 2022, 10(10): 1653. https://doi.org/10.3390/math10101653

12. Ilka R, Alinejad-Beromi Y, Yaghobi H. Cogging torque reduction of permanent magnet synchronous motor using multi-objective optimization[J]. Mathematics and Computers in Simulation, 2018, 153: 83-95.

13. Wu S, Huang X, Tian C, et al. Multi-physical field optimization analysis of high-speed permanent magnet synchronous motor based on NSGA-II algorithm[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS). IEEE, 2019: 1-6.DOI: 10.1109/ICEMS.2019.8922236

14. Zhao W, Wang X, Gerada C, et al. Multi-physics and multi-objective optimization of a high speed PMSM for high performance applications[J]. IEEE Transactions on Magnetics, 2018, 54(11): 1-5.DOI: 10.1109/ICEMS.2019.8922236

FINANCING

No financing.

CONFLICT OF INTEREST

None.

AUTHORSHIP CONTRIBUTION

Methodology: Anton Louise De Ocampo.

Software: Rowell M. Hernandez.

Supervision: Celso Bation Co.

Drafting - original draft: Fengmei Shen, Celso Bation Co.

Writing - proofreading and editing: Fengmei Shen.