Modeling performance evaluation in badminton sports: a fuzzy logic approach

doi: 10.56294/sctconf2024986

Category: STEM (Science, Technology, Engineering and Mathematics)

ORIGINAL

Modeling performance evaluation in badminton sports: a fuzzy logic approach

Modelización de la evaluación del rendimiento en deportes de bádminton: un enfoque de lógica difusa

Yinghao Li^1,2 *, MN Jawis¹ *

¹Exercise and Sports Science, School of Health Sciences, Universiti Sains Malaysia. Kota Bahru 16150, Kelantan, Malaysia.

²Department of Physical Education, Zhengzhou Shengda University. Zhengzhou 451191, Henan, China.

Cite as: Li Y, Jawis MN. Modeling performance evaluation in badminton sports: a fuzzy logic approach. Salud, Ciencia y Tecnología - Serie de Conferencias. 2024; 3:986. https://doi.org/10.56294/sctconf2024986

Submitted: 03-02-2024 Revised: 30-04-2024 Accepted: 29-06-2024 Published: 30-06-2024

Editor: Dr. William Castillo-González

Corresponding author: MN Jawis¹ *

ABSTRACT

Spectators and many young students have flocked to badminton matches in recent years. Badminton practice has received a lot of media coverage. The current state of badminton evaluation methods is lacking in reliability. This article’s overarching goal is to examine the many applications of fuzzy logic in badminton performance evaluation and improvement. Data on the badminton technique’s flexion and extension phases are mapped into the suggested model using a fuzzy inference system (FIS). This study suggests a fuzzy logic-based badminton-specific objective fuzzy inference system (Bmt-FIS) to evaluate team sports. Despite the gravity of the situation, decisions involving performance reviews often use subjective data. These common decision-making problems may be realistically addressed by fuzzy logic models. Fuzzy logic has the potential to be an effective tool in situations where both quantitative and qualitative data interpretation are allowed. To do this, it accounts for the inherent variability in athletic performance by taking into consideration the ‘hazy’ or ‘uncertain’ limitations of data. By taking limitations into account, a rule-based approach makes performance evaluation more precise. Here, a fuzzy inference system (FIS) uses the input variables to evaluate the student’s performance. While data mining approaches have been studied, the adaptive neural fuzzy method outperforms others because of its exceptional accuracy.

This method eloquently and clearly conveys the many levels of integrity and ambiguity. Also, fuzzy logic may be a great tool for evaluating badminton skills. This foundational study connects the dynamic realm of sports with static measures.

Keywords: Fuzzy Inference System; Neural Fuzzy; Adaptive Neuro-Fuzzy Inference System; Fuzzy Logic.

RESUMEN

En los últimos años, los espectadores y muchos jóvenes estudiantes han acudido en masa a los partidos de bádminton. La práctica del bádminton ha recibido mucha cobertura mediática. El estado actual de los métodos de evaluación del bádminton carece de fiabilidad. El objetivo general de este artículo es examinar las numerosas aplicaciones de la lógica difusa en la evaluación y mejora del rendimiento del bádminton. Los datos sobre las fases de flexión y extensión de la técnica del bádminton se mapean en el modelo sugerido utilizando un sistema de inferencia difusa (FIS). Este estudio sugiere un sistema de inferencia difusa objetivo específico del bádminton basado en lógica difusa (Bmt-FIS) para evaluar los deportes de equipo. A pesar de la gravedad de la situación, las decisiones que involucran evaluaciones de desempeño a menudo utilizan datos subjetivos. Estos problemas comunes de toma de decisiones pueden abordarse de manera realista mediante modelos de lógica difusa. La lógica difusa tiene el potencial de ser una herramienta eficaz en situaciones en las que se permite la interpretación de datos tanto cuantitativos como cualitativos. Para ello, tiene en cuenta la variabilidad inherente al rendimiento deportivo teniendo en cuenta las limitaciones “confusas” o “inciertas” de los datos. Al tener en cuenta las limitaciones, un enfoque basado en reglas hace que la evaluación del desempeño sea más precisa. Aquí, un sistema de inferencia difusa (FIS) utiliza las variables de entrada para evaluar el desempeño del estudiante. Si bien se han estudiado enfoques de minería de datos, el método neuronal difuso adaptativo supera a otros debido a su precisión excepcional.

Este método transmite de forma elocuente y clara los numerosos niveles de integridad y ambigüedad. Además, la lógica difusa puede ser una gran herramienta para evaluar las habilidades del bádminton. Este estudio fundamental conecta el ámbito dinámico de los deportes con medidas estáticas.

Palabras clave: Sistema de Inferencia Difusa; Neural Difuso; Sistema de Inferencia Neuro-Difuso Adaptativo; Lógica Difusa.

INTRODUCTION

Badminton has become more popular among students and the general public in recent years. Many people in the training and education sector are worried about badminton’s rise to prominence and prospects.⁽¹⁾ Pastors also uncovered many innovative and valuable training techniques throughout the research and development. Unfortunately, most of the badminton education studies conducted so far have concentrated on collegiate badminton programmes and professional sports team instruction.⁽²⁾ Research on public and youth training and education approaches is lacking. While badminton is an excellent way for young people to be in shape as it uses every muscle in the body, the sport has suffered from a lack of organised instruction and poor technology that could record players at their best. Consequently, filling this gap via research into effective adolescent teaching techniques is a vital responsibility.^(3,4)

In recent years, massive shifts in performance analysis within sports science have occurred, mainly due to more accessible access to better technology and more applications within computer science.⁽⁵⁾ Using professional analysts does not eliminate the constraints of notational analysis or coding in sports. These approaches usually take time, are subjective, and are vulnerable to prejudice and human error.⁽⁶⁾ The use of automated movement recognition in sports and its integration into code has the potential to greatly improve the accuracy and efficiency of sports performance monitoring. One of the most interesting badminton research is the modeling of the evolution of positional information about players and their strokes.⁽⁷⁾ Visualizing performance patterns helped participants in one research comprehend the context of their opponents’ victories. Using video analysis to examine performance during matches is a rare occurrence; even fewer research have focused on collecting shuttlecock trajectories and classifying serves and strokes.⁽⁸⁾ Video analysis documents badminton strategies in relation to court location, opponent strength, and stroke type (i.e., technical motions) using performance models derived from classification and detection data. There has been no incorporation of opponent-related actions based on space and success for badminton, despite this first method to analyse player’s performance patterns/profiles.^(9,10)

The fast reactions needed to execute intense high-intensity moves involving a shuttlecock travelling at high speeds without touching the ground (as in volleyball) set badminton apart from other racket sports (like tennis or paddle).⁽¹¹⁾ As a result, non-linear, contextually related, multivariate approaches pertinent to the opponent’s performances should be included in performance analysis and interpretations. Without considering the context of the player’s placement during performances, isolated variables (such as technical-tactical indicators) might lead to misleading results.⁽¹²⁾ In badminton and other racquet sports, players must constantly assess their opponent’s limitations in terms of space, speed, and playing actions and adjust their attacking and defensive strategies.⁽¹³⁾ A traditional method is used to evaluate students’ performance by the norms and regulations of an institution. To determine if there is a difference in real-world data, the findings produced by the expert system and the traditional technique are compared and tested.⁽¹⁴⁾ To assess students’ progress, the research suggests using fuzzy logic techniques and comparing their findings to those of more traditional approaches. The student’s performance is evaluated using the sample study.⁽¹⁵⁾ According to studies conducted on evaluations, fuzzy logic and more traditional approaches provide varied results. When compared to standard back propagation neural networks or more conventional statistical models, a fuzzy probabilistic model may better predict how well individual students will do and then classify them accordingly.⁽¹⁶⁾ Using a traditional fuzzy logic framework, the fuzzy evaluation system suggested an evaluation method for linguistic hedges (LHs). Fuzzy rules and empirical assessment form the basis of the evaluation, and the findings demonstrate insignificant comparisons between linguistic hedges (LHs) and conventional fuzzy logic.⁽¹⁷⁾

This study provides a novel methodology for assessing sportspersons’ work that uses fuzzy logic reasoning. For a more accurate assessment of students’ abilities, this research considers their academic success and personality attributes. One of fuzzy logic’s many advantages, as shown in the research, is the ability to give distinct traits differing weights.⁽¹⁸⁾

The main objectives of the paper are as follows

The suggested approach considers both the location of the shuttlecock and the player’s performance data, which together better represent the player’s decision-making process throughout a match. Applying fuzzy theory combined with the basic parameters, we may construct a new prediction model of badminton sports performance outcomes, using optimization as the basis. Compared to approaches that relied just on players’ actions and ways that used both shuttlecock and player performance data, the suggested Bmt-FIS method is more accurate. The next steps are as follows: phase 2 will discuss the literature review; phase 3 will examine the recommended technique; phase 4 will talk about the numerical findings and analysis; and phase 5 will wrap up the paperwork and plan for future work.

Related literature

The practicability of a smartphone-based measuring system for badminton six-point footwork was assessed by Ya-Lan Chiu et al.⁽¹⁹⁾. Thirty badminton players had their smartphones fastened to their belly buttons and used a custom program to track their acceleration while they performed the six-point footwork. In all except the frontcourt orientations, badminton players’ mean and maximum acceleration were higher when they completed their footwork quickly. The present research established that badminton footwork can be evaluated using a smartphone’s built-in accelerometer. The goal of the cheap visual response system that Kuei-Pin Kuo et al.⁽²⁰⁾. Created for badminton instruction was twofold: first, to gauge and enhance badminton players’ footwork and movement, and second, to provide valuable reference data. The training system’s training and assessment activities remained steady and dependable for long periods. The results demonstrated that players’ agility and visual response time were significantly enhanced. The suggested training system is an inexpensive alternative for training and tracking, assessing, and documenting training results. Using an indoor badminton court simulator, Ping Huang et al.⁽²¹⁾ recorded the maximum right lunge movements of 16 badminton players (eight pros and eight amateurs). They compared them using an injury mechanism model. This procedure examines the variations in kinematics and joint moment between the right ankle and knee. This research recreates an artificial badminton court and adjusts the range of motion for each person so that they can do the experiment as naturally as possible while maintaining a high level of quality. Ye-Jin Zheng et al.⁽²²⁾ used microelectronics and additive manufacturing with lightweight components and safety issues to design, produce, and insert two capacitive sensor units onto two matching finger stalls. By linking the sensing units to an adaptor and finally to a transmission port, this study sought to build a wireless force sensing system for application in sports science. These findings broke new ground in sports science by showing that the proposed method outperforms the competition and can distinguish between players with various skill levels while also determining if their attitude is stable or changeable. LI Yunwei et al.⁽²³⁾ used an adaptive threshold technique based on particle filter prediction to accomplish the adaptive separation of moving objects. To build the motion model, we use particle filter technology to follow the athletes’ paths. To follow the next frames of the moving movie, this is used to forecast where the critical joints will be in the following frames. The badminton tutorial video primarily use the conditional random field method for motion recognition, which increases the recognition rate and decreases the false separation rate. The keyframe detection module, as proposed by Muhammad Atif Sarwar et al.⁽²⁴⁾, examines the activity frame sequence and finds keyframes for each micro-level action, such as start, ready, strike, and finish. To better understand the complicated macro-level action, this framework breaks it into smaller parts and examines each separately. Finally, in order to separate specific activities, the modules that detect movement and posture review the data obtained from various sources. When it comes to products that use this platform, CoachBox is one example. Using the dataset’s mean absolute error, we assess the suggested framework. Researchers Rahmad et al.⁽²⁵⁾ suggested utilising a pre-trained Convolutional Neural Network (CNN) approach to develop an automated system that can recognise badminton smashes in publicly accessible broadcasted footage. The footage was used to train CNN models to mimic badminton smash, clear, drop, lift, and net actions. When it comes to detecting smash actions, the pre-trained GoogleNet model clearly stands out. As a result, a pre-trained AlexNet model can automate all five badminton operations, and a GoogleNet model can detect the smash action in broadcasted films with ease, paving the way for more insightful analysis.

METHOD

Modelling for student performance assessment requires a shift in current evaluation standards, yet it has several uses in educational institutions to raise students’ learning standards. To forecast badminton players’ performances, a fuzzy logic model is built around a multitude of physical data based on different attributes. Enthusiastic learners work hard to achieve objectives within their current learning capacity and advance according to the merit of their achievements. Assessed by the standards for claiming performance, making strides towards quality work, and putting in extra effort to ensure quality work. The ability of the student to solve problems is broken down to choose the optimal action to take. Badminton students’ overall performance is impacted by how they are evaluated while working in groups or on teams. They are well-known for the consistency with which pupils present them in the classroom or at work. We may learn much about students’ progress from their responses to various forms of supervision, reflection, diversity appraisal, entrepreneurial introduction, written and spoken communication, interpersonal communication, etc.

Figure 1. Shuttlecock trajectory using fuzzy model

This study suggests a way to forecast where a shuttlecock will go in the subsequent frames using the current location of the shuttlecock as well as the positions and postures of the two competitors observed in the previous frames. Figure 1 shows the two main components of the suggested approach: one for detecting and estimating poses in previous frames and another for making predictions using a time series model. The first module takes a video feed of badminton matches as input and processes each frame individually, detecting shuttlecocks and players and estimating their poses. The second module precisely aligns the player’s posture, shuttlecock, and player position in two dimensions. After that, the six-dimensional data is inputted into the trajectory prediction system.

Recognising and Estimating Pose from Previous Frames

A shuttlecock detector, like TrackNet, is used to get the location information of the shuttlecocks. The coordinates 𝑥𝑏 and 𝑦𝑏 on the picture are two-dimensional. Several pose estimation and pre-trained models are used in the MMPose framework for player identification and posture estimation. A model that evaluates the players’ posture and records their key points finds the players and stores their locations as bounding boxes. Using ANFIS, we apply an object detector to recognise people. Due to its detection process, the detector gives you bounding boxes and confidence ratings. When a rectangle encloses a person in a picture, four two-dimensional coordinate points depict the bounding box. The confidence score indicates the probability that the identified item within the bounding box is a person, which might be anything from 0 to 1. The confidence score is useful for identifying players alone rather than officials or onlookers. The trust score of referees and spectators identified with players is lower because they may be seated, their faces might be the only thing in the picture, they might be facing the wrong direction, or they might be tiny. Therefore, the player is determined by tallying their confidence score, and their bounding box is produced.

The normalised centre coordinates (i_player,j_player) of the player are calculated for each coordinate in the way to acquire the player’s location information is shown in equation (1):

Assigning a number to each player in the photograph helps to recognise them, beginning with the player on the bottom side. The four-dimensional coordinates (i_f1, j_f1, i_f2, j_f2) indicate the player’s location information. In this case, i_f1 is the i-coordinate of the player seen at the bottom of the picture. The picture’s absolute coordinates are used to represent the coordinate values. The normalised absolute coordinates ki_a, kj_a of a keypoint are determined using the values in figure 1; for instance, if the keypoint’s image coordinates are (i_a, j_a). If the input image’s width is k and its height is by a, then equation (2) is accurate. The two players’ posture data is provided as a 68-dimensional feature vector (i_f1a1, j_f1a1,…, i_f2a15, j_f2a15) where is the i-coordinate of the first keypoint of the player depicted on the bottom of the picture.

Future Prediction Using a Time Series Model

To make trajectory predictions, the suggested technique takes three kinds of data: the location of the shuttlecock as detected by the shuttlecock detector, the position of the player as detected by the object detector, and the player’s posture as estimated by the pose estimation. Currently, there are two dimensions to the data on the shuttlecock’s location, four dimensions to the data on the player’s position, and sixty-eight dimensions to the data on the player’s posture. As indicated in figure 1, three different sources of information are transformed into a space-specific feature vector by including each in two dimensions via an ultimately linked layer. A 6-dimensional feature vector is created by combining the position data of the shuttlecock with the position data of the player and the posture data of the player.

To predict the future of badminton is shown in figure 2. The overall flight trajectory forecast is unaffected by the small variations in the locations of the spots on the shuttlecock in space. This paper’s trajectory forecast uses the shuttlecock as the centroid and the median of the disparity map as the centroid’s parallax. Here is the formula to calculate the coordinates in three-dimensional space: the equation (3) may be written as:

[I J F S]=W[i j c 1 ],W=[1 0 0 -V_i 0 1 0 -V_j 0 0 0 p 0 0 -1/G_i (V_iq-V_ie )] (3)

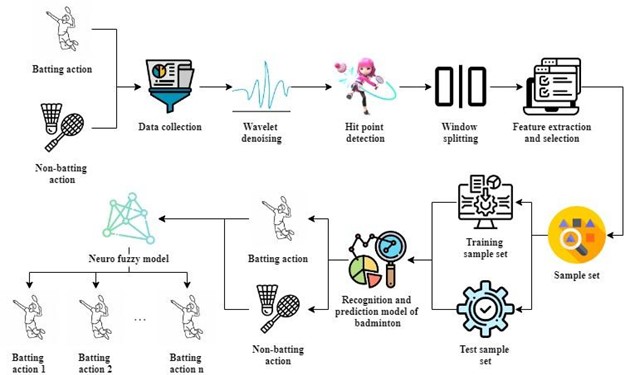
Figure 2. Intelligent performance analysis of action data

At the badminton centroid in the left picture, where i and j are the pixel coordinates, c is the parallax, and the three-dimensional coordinates of this point are (I/S,J/S,F/S). To keep things simple, this article will assume that V, ρ, and S remain constant while the badminton shuttlecock is in flight. In badminton, the force is split as follows in equation (4):

{k_iy=p_i=p sin sin φcos cos θ=-ac_i² k_jy=p_j=p sin sin φ cos cos θ=-ac_j² k_l y=p_l=p sin sin φcos cos θ=-ac_l²-yh (4)

This simplifies the computation. The precision of the measurement determines how well the least squares technique estimates. The findings generated by the least squares approach will be distant from the genuine value if the collected data includes substantial amounts of noise. Unevenness characterises badminton. An inaccurate centre of mass estimate has been made. Additionally, there is an inaccuracy in the parallax calculation since the camera’s resolving capabilities decrease with distance. To enhance the precision of badminton’s kinematics equation solution, it’s essential to pre-process the space track location of the empty wool ball to lower data noise. We see badminton using the x-axis movement to build an extended Gaussian filter. The state equation of the extended Kalman filter is given in equation (5):

We can expand the Taylor series of (i_a-1, o_a-1, q_a-1) and d (i_a, w_a), and take a term to obtain:

In equation (6), the i and j directions, for movement q_a-1=0, and in the l direction for movement Q=[0 0 1]^G and q_a-1=-h. One way to get the badminton straight path closer to its actual value is to use an extended Kalman filter to filter it.

Building a Video Image-Based Performance Detection Model

The following steps are used to extract face, non-face, and partial face samples:

Step 1: take the labelled data and randomly choose several frames from Wider_face to use as candidates for the performance calculation. A face is the candidate area if the value is more significant than 0,65.

Step 2: border data will be present for some face data, and data that is more significant than 0,4 but less than 0,65 is considered face data; data that is less than 0,4 is considered non-facial data. When all the necessary components are in place, the video’s actual face identification process may start. Create an image pyramid as a starting point. Simply input the image and use the equation (7) provided to get the size of the modified image:

min_M=org_M(12/minsize) factor^x, x=[0,1,2,3,…,X] (7)

The number of images that can be shrunk is equal to x. The picture stops zooming when its length or breadth approaches 12, the minsize is the smallest observable image, and the factor is the zoom factor while building the image pyramid. It should be noted that the zoom size cannot be smaller than 12.

Step 3: load the picture into Pnet, the first-layer network. Incorporate the images from the previous step’s image pyramid into this layer’s neural network training. Then, the face score and boundary regression results will be collected. In order to eliminate the sliding box with a score lower than the threshold (0,6), the face score is first obtained and then filtered accordingly. After the screening process, the FIS approach combines the candidate boxes that were kept.

Step 4: apply additional in-depth image processing using the Rnet layer, then score and filter the face frame acquired by Pnet again. To finish the job, the face frame output from the P network has to be extracted from the original picture, reduced in size to 24*24*3, and then inputted into the Rnet network layer.

Several unreliable users contribute to the badminton motion signals’ total surface area and strength. The vibration interval is separated into segments during the badminton motion segmentation process. At the sports motion pause, every badminton motion signal was superimposed onto the most extended signal to reduce the impact of human distinction. After that, people standardise the sports data by using techniques to reduce the differences between the two users within a single amplitude. Equation (8) represents the standardisation of the a-score type.

Where the signals VL(e) and VL_i (e) represent the original and normalised badminton sports movements, respectively, inside the badminton motion interval, there are time stages inside a sport motion interval. The mean and standard deviation of the sports motion signals throughout the badminton motion time are represented by VL_mean and VL_std, respectively. Once have all the data from the spectrogram, use a linear adjustment to split it into equal-length samples. Then, the Fourier analysis for each group will be determined separately. The following is how badminton’s VG, or normalisation of motion signal, is calculated in equation (9):

The normalised badminton motion signals are represented by x[i], the pixel value is denoted by [φ], and the window stored procedure centre is denoted by j in the representation using the VG. The VG is computed using a modulated signal that connects with a 60 % accuracy and a changing point transform. By dividing the amplitude of the recovered X features by the square of the normalised badminton signals’ VG, we get equation (10):

With the exact image resolution as the input data from the convolutional layers, the output data of a convolution operation is established utilising the parameters set more by the convolutional m. As indicated in the following equation (11), the signals that come out of the convolution layers are first called extracted features.

The equation still represents the size and shape of the runtime environment through R and x, but K is the surface index. p_K^X is the most biassed type for the pth feature in the K^th layer’s space, and R_j,i^X,K and i do have a relationship with the information i_(x+j+i-1)^(X-1,K) according to the pth feature type of space of the X^th layer. The same holds for equation (12), which is to the kind of separated function.

For (0,g) , we may derive equation (12). The maximum pooling operation used in this study may be calculated using equation (13). Among neighbouring extracted features, it also offers the most value.

The accumulation size is denoted by O_x×D+0,y_×D+0^X,K and the running style is represented by A=2. Furthermore, this one-dimensional classification model is made by omitting the phase of convolution, and the data for this comprehensive layer, QIc fundamental features, are supplied from the tightly packed, fully connected layers, as shown in the following equation (14):

Softmax, the final crucial frame performance metric, evaluates several sports classes and an over-anticipated posterior distribution is shown in equation (15).

Figure 3. Design of Fuzzy Inference Systems

The components of a fuzzy inference system (FIS) include algorithms for fuzzification and defuzzification, fuzzy rules, and input-output membership functions based on fuzzy logic. Figure 3 provides a summary of the whole fuzzy inference system. The system uses fuzzy rules to process inputs and fuzzy logic concepts to generate outputs. The fuzzy models were developed using the MATLAB B® programme and associated packages. The idea was to make a file with a fuzzy inference system, load it with the correct starting script, and then run its assessment on each input data file for municipalities. The goal of the suggested models is to analyze an athlete’s performance using ranking data. This research utilised badminton data to present mathematical models. Badminton has a lengthy history as an individual sport, and it has even made it to the Olympics. Because the BWF is transparent about its rankings, the models can access massive datasets, including head-to-head statistics on the best players. As a goal, every coach or player chooses which events they would want to compete in, considering the athlete’s level. Making decisions on organising tournaments has always been challenging due to the specific objectives. Because of the unique goals, deciding how to organize tournaments has always been difficult. When an athlete is first starting, they may assume that entering many competitions is the way to go. Nevertheless, this is impractical since players must perform admirably in every competition, necessitating extensive training. In addition, while preparing for a season, coaches must make difficult choices to get enough points and a respectable ranking.

Assessed and evaluated using a model based on fuzzy algorithms for quantitative analysis

The binary logic {0,1} should be expanded to include the interval [0,1]. The feature function should also be extended to encompass the membership function μS(i)ϵ[0,1], and μS(i) should be allowed to belong to the interval. To characterise the fuzziness of objective objects’ intermediate transition, use this feature function. The following equation (16) is the factor set H={h₁, h₂,…, h_y}, which arises from the fact that y distinct factors impact the result of a particular object. One needs to record the mth factor’s single factor evaluation fuzzy set S_m=s_m1, s_m2,…, s_mn. The next step is to get the m-factor single-factor evaluation matrix.

S={R₁₁ R₁₂…R_1n R₂₁ R₂₁…R₂₁…………..R_m1 R_m2 …R_mn (16)

Consequently, the equation (17) is represented by the fuzzy comprehensive evaluation set. Would it be possible to give the most assistance in organising variables according to the opinions of m experts? The final product is a table with rows and n columns; the elements of the table are . The th component’s rank sum is represented by the function . To get the weight of the th element, we may use the following formula:

Where G_y is the weight in the equation (17). Fuzzy design may provide a more complete picture of its pros and cons, even if it relies heavily on multifactor analysis and weighting. However, of the emphasis they place, the two are distinct. An important part of the cross-impact analysis method is looking at the variables and their importance. Evaluation of the end product is the main emphasis of the fuzzy design analysis method.

The first step is to construct a model for the evaluation index system that measures the competitiveness of badminton players. The complicated challenges are organised and treated hierarchically using the specified model. The four levels of competitiveness—first-level, second-level, and third-level indicators—are based on this research. The second step is to create a comparison judgement matrix that uses pairs, as shown in equation (18).

Next, we have the positive reciprocal matrix or pairwise comparison matrix D is given in equation (19):

In the third stage, the weight vector is calculated. Next, the greatest eigenvalue of the judgement matrix and the feature vector Q_x are computed. Its formula for computation is given in equation (20):

It is often believed that the computed weights may be recognised when FI<0:1, which is shown in equation (21):

Effectively dividing the game outcomes, such as home win and draw, may assure the efficacy of the prediction model. The data kinds are then divided using the standard, and the model’s validity is checked using the data matrix, allowing for an adequate identification of the number of contests. Data sets do not need to be perfectly balanced throughout the assignment process. As a result, the assessment logic will depend on how accurate the classification is. The performance assessment and prediction findings may be more relevant when the data is imbalanced. Optimising the storage of training data is crucial in sports prediction. As seen in figure 4, the cross validation approach may be used to compare future sports predictions to prior ones. Figure 4 shows that data prediction will mess with the order of different data types. In sports performance prediction, cross validation is determined to have great applicability.

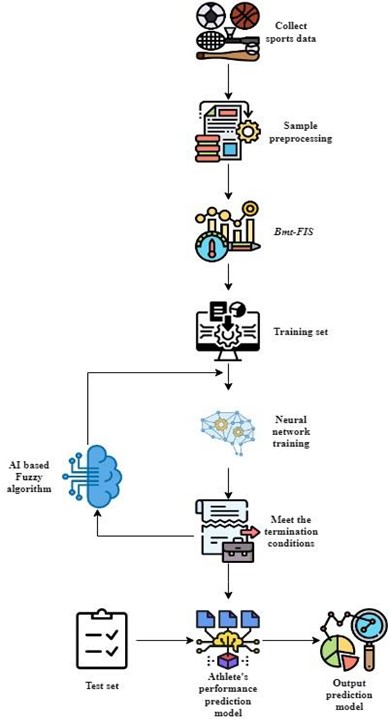
Figure 4. Working principle of proposed Bmt-FIS

Allocation of Models

Model matching frequently requires no human interaction. The data unit receives several sports data types easily. The network architecture gets this data. After updating the training and detection data, the forecasters will execute a new data training approach, acquire the data training model, achieve a new performance matching result, and transmit the matching result as prediction information. After completion, the data unit receives further data. The new learning unit’s design allows it to gather important data efficiently throughout every athletic event. Increasing the quantity and amount of new training data is continuous. The dynamic flexibility of this categorization unit shows it may accurately represent athlete development.

Experimental Approach to Scheme Verification

An Algorithm for Sports Data. The dynamic variability of sports personnel’s performance is heightened by several elements, including the physical quality of members, the quality of coach curriculum design, sports training techniques, training instruments, applicable legislation, and the national economy. The sports performance of sports members is largely correlated with the sports information in the present period within a specific timeframe. To uncover the hidden qualities of different sports accomplishments, it is possible to use chaos theory to study the dynamic features of performance data from athletes. The number of nodes collecting data is represented by the score expression, {p(e_y), y=1,2,…x},x is the available sports personnel score in a period. Using fuzzy theory, motion data may be handled efficiently, leading to conclusions that reflect changes in the data, as shown in equation (22):

According to equation (22), this variable indicates the embedding dimension of certain sports participants and the delay time of their information. As part of this, it’s possible to use the m parameter to relay the internal connection between all of your data sets and the most recent sports scores. One by one, the E and y values corresponding to the sports members’ information are delivered using FIS algorithms to feed back the changing law of the performance information concealment of the members of the sports.

Applying equation (23), we can get the distance between the two sets of score information, given that the two example nodes of a single athlete’s performance are:

The equation may be rewritten as:

In equation (24), we add the critical radius parameter is E, and to represent the data fraction of each point in this critical region, we utilize the correlation integral V. The process of specific description is shown in:

In equation (25), the expression of Ub-‖P(n)-P(m)‖ is a Heaviside function, and X denotes the data specification. This function’s computation technique is shown in the following:

Effective processing and division of sports participants’ performance into branch sequences are made possible by the aforementioned approach. The resultant expression may be seen in equation (26):

The formula for finding the difference between the highest and lowest values in a branch series is given in equation (27):

The expression processing is shown if the sports performance y value of the athletes is 1-s is given by equation (28):

A single badminton sports member’s score data set is retrieved. The vector parameter with the shortest interval is P_y(n+y)(y=1) and the reconstruction vector parameter for the n location is P_n (y=1), as shown in equation (29):

The y-value acquired at this moment may be utilised as a fair value for the performance prediction of badminton sports persons when the result of equation (29) is the minimum parameter and the variable range of the parameter is modest. Here is the equation (30):

The findings with high performance and classification outcomes and the conclusions gained suggested fuzzy approaches as another viable option for evaluating executed tasks. These techniques are more basic but still successful. Applying suitable segmentation processes and computations, breaking the data into single repetitions and extension, flexion, and holding phases, allows for the automated estimation of such determinants. The fundamental use of the concept is the compression and summarization of data via granulation. The primary benefit is that the FIS can process input data of any kind, regardless of how noisy, distorted, or inaccurate it may be. The structure of FIS is easy to understand; thus, making modifications to FIS is very simple. The mathematical principles of set theory provide the basis of fuzzy logic, and their reasoning is simple. It can effectively answer complex issues in every area of life as it mimics human thinking and decision-making.

RESULTS

Adding new rankings for racquet sports might tweak the optimal model. Even though the optimised model was much better at picking tournaments and adding them to the planning process, some limits remain to consider. Given the frequency of occurrences occurring on consecutive weekends, 52 weeks provides enough time for accurate forecasting. To enhance performance, you may either train the system on more data sets or increase the maximum number of generations for optimization. The model’s datasets are open source and available to everybody, so anybody may put the proposed systems into action. This is one approach to model development that aims to bridge the gap between big teams with unlimited resources for performance monitoring and smaller clubs with a single coach juggling many responsibilities. This method is helpful for players since it allows them to assess opportunities very instantaneously. Unlike bivalent logic, fuzzy logic has a far greater degree of generality. The foundation of many of fuzzy logic’s practical benefits is its generalizability.

Dataset Description: adataset with pictures of several sports classes is given to you. Separate sets of data are used for training and testing. Cricket, wrestling, badminton, tennis, soccer, swimming and karate are the sports included in the training package. Every image has a distinct picture ID and a matching class label. You are required to provide a classification prediction for each of the unlabeled photos in the test set.

Actions during play analysis

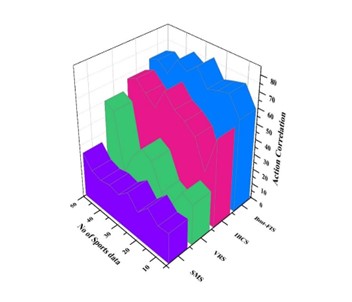
Figure 5. Actions during play analysis

It is impossible to discuss the relevance of these factors since there has been no research on them. Due to the lack of evidence of a player winning a set with significantly more unforced errors than their opponent, results demonstrating a correlation between set win/loss and unforced error count and winning shot percentage are intriguing. With some matches included in this research, the player with fewer unforced mistakes won the set in 77,1 % of the instances, while the player with the most unforced errors won in just 22,9 % of the situations. In terms of statistical analysis, however, the apparent contradiction revealed by these data is not significant (see Figure 5). The reason why there is a negative correlation between the number of maximum actions and both the average and maximum heart rates when it comes to maximum actions is that a higher heart rate reduces the capacity to perform at maximum intensity, leading to fewer maximum actions because the level of response is too low to carry them out.

Accuracy ratio

Table 1. Accuracy ratio
No of Sports data	SMS	VRS	IBCS	Bmt-FIS
5	21,3	31,1	58,4	79,4
10	29,6	36,2	56,8	82,5
15	18,7	32,6	31,9	79,6
20	19,4	21,6	52,4	68,3
25	16,4	28,7	61,2	59,7
30	25,4	48,3	53,1	62,7
35	19,3	49,6	63,4	72,1
40	23,1	41,6	61,9	68,2
45	24,5	52,3	62,3	72,5
50	16,4	49,6	63,7	76,4

The percentage of correctly categorised scenes (true positive and true negative) out of a total number of video scenes is known as accuracy in football video scene classification. Because of this, accuracy is determined by equation (31):

In this case, the correctly identified shots of positive (P) classes are called true positives (TP). Correctly identified negative (N) class photos are called true negatives (TN). Figure 6 shows the suggested Bmt-FIS model’s accuracy ratio. Integrated within the badminton racquet is a separate speed sensor that tracks the game’s movements. In order to determine its goal-scoring signal’s properties, the suggested method is used. By contrast, the suggested Bmt-FIS method demonstrates that badminton training yields better results for athletes in terms of overall accuracy and time. The new algorithm outperforms the current technique by seven percent in terms of overall accuracy (refer to Table 1). Wearable and non-wearable technology, as well as certain internet-enabled mobile apps, may enhance this training. Most coaches recommend these methods and resources for keeping tabs on player activities.

Performance ratio in sports

Tactical data is crucial for evaluating a team’s game performance and forming the foundation for player training and game decision analysis. Statistics ignore geography and time since they focus on players, their on-field behaviours, and their game success. Stats include free throws, shooting tempos, and scores. There are free throws. Simply watch the game data to see how each team fared. The program provides comprehensive overviews of full games and enables users to go deeper into certain events or subjects. Team statistics include shooting distances, free throw percentages, mistakes, and other numerical measures of performance and effectiveness. In competitive sports data vision research, team data is called “battle array” or “tactical information”. Teams use it to compare and contrast work. Figure 6 displays the ratio of sports performance.

Team statistics include shooting distances, free throw percentages, mistakes, and other numerical measures of performance and effectiveness. In competitive sports data vision research, team data is called “battle array” or “tactical information”. Teams use it to compare and contrast work. Figure 6 displays the ratio of sports performance.

Figure 6. Performance ratio in sports

Efficiency ratio

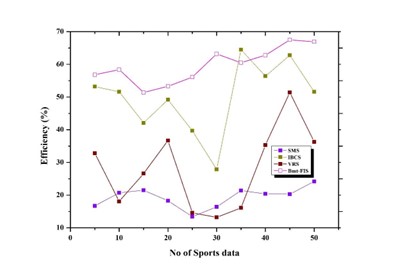
Figure 7. Efficiency ratio

It is usual practice to analyse a player’s performance and contribution using possession statistics and shooting information. When the player discharges a time series at a specific coordinate point, it is considered an action and an event in the game world. Substitutions, off-court problems, assists, robberies, mistakes, and other occurrences are also available. There have been a lot of studies looking at players’ numbers to see whether they have improved their defensive effectiveness over time. Consequently, time series events provide an additional metric for gauging the impact and performance of players. Most visualisations of sports data centre on the primary indication, which also serves as the foundation for analysing player behaviour patterns. The efficiency ratio of the suggested Bmt-FIS model is shown in figure 7.

To evaluate the effectiveness of the proposed Bmt-FIS model derived from neuro fuzzy model, this research used objective measures. As a result, the performance was evaluated using the following criteria: accuracy, performance, efficiency, and play-action analysis. Furthermore, these metrics are computed regarding the precise or improved categorization of data kinds for every recording assessment. The last step is to get the conclusion value by taking the average of the results obtained from all of the different categories of videos or images.

CONCLUSIONS

Fuzzy inference systems employ a rule base to determine or infer from the system’s output; a thorough description of these systems was a theoretical undertaking. Inference systems for uncertain data rely on these systems as a substitute for expert knowledge of the relevant situation. They provide the groundwork for a reliable fuzzy regulator. An important example of analytical bias would be a coach concluding an athlete based on their previous views and then interpreting the results to confirm those preconceptions. The ideal model may be fine-tuned by including updated rankings for racquet sports. Even though the optimized model did a better job of choosing which tournaments to include in the planning, it is still vital to think about limits.

At the very elite level, badminton requires a great deal of aerobic power from every player. Accurate monitoring of player trajectories is crucial in badminton. This work uses the fuzzy inference system approach to implement a badminton performance evaluation system. All of the evaluation criteria are measured scientifically using this technique. After constructing a fuzzy consistency matrix to evaluate the indicators’ significance levels, we get a respectable research outcome. The Bmt-FIS evaluation strategy has the potential to compensate for the absence of badminton performance evaluation by raising the bar for badminton education and teaching quality. People may be able to accomplish enough to prepare for forthcoming sports and computer methods by using this idea as a real-time program. It is strongly advised that sensor approaches be used to analyse badminton performance in future studies.

The most critical metric for measuring the competitiveness and skill level among athletes and students is their performance on the pitch. Athletes’ and students’ physical abilities aren’t the only variables affecting their success on the pitch; training techniques and other influences also play a role. Many variables may affect athletes’ performance, and the results may be unexpected. Performance analysis using an adaptive neuro-fuzzy inference system provides trustworthy data on athletes’ abilities across levels. First, we collect all the information we can about a player’s performance in a specific period and find a connection across time frames. The study aims to predict a participant’s future performance by examining their current performance and how it fluctuates in sports. Bmt-FIS may enhance performance prediction and evaluate the learning network’s connection weight and threshold. Finally, when real athletes check the simulation’s accuracy, the prediction model’s utility is assessed.

ACKNOWLEDGEMENT

2024 Henan Province Teacher Education Curriculum Reform Research Project---Research on the Digital Construction Path of Physical Education in the Higher Education Institutions of Henan Province (2024-JSJYYB-133).

BIBLIOGRPHIC REFERENCES

1. Taha Z, Hassan MSS, Yap HJ, Yeo WK. Preliminary investigation of an innovative digital motion analysis device for badminton athlete performance evaluation. Procedia Engineering, 147, pp. 461-465.

2. Shi W, Lai JH, Chau CK, Wong P, Edwards D. Analytic evaluation of facilities performance from the user perspective: Case study on a badminton hall. Facilities, 39(13/14), pp. 888-910.

3. van de Water T, Huijgen B, Faber I, Elferink-Gemser M. Assessing cognitive performance in badminton players: a reproducibility and validity study. Journal of Human Kinetics, 55(1), pp. 149-159.

4. Abián-Vicén J, Sánchez L, Abián P. Performance structure analysis of the men’s and women’s badminton doubles matches in the Olympic Games from 2008 to 2016 during playoffs stage. International Journal of Performance Analysis in Sport, 18(4), pp. 633-644.

5. Loureiro LDFB, Dias MOC, Cremasco FC, da Silva MG, de Freitas PB. Assessment of specificity of the badcamp agility test for badminton players. Journal of Human Kinetics, 57(1), pp. 191-198.

6. Ghosh I, Ramamurthy SR, Roy N. Stancescorer: A data driven approach to score badminton player. In 2020 IEEE international conference on pervasive computing and communications workshops (PerCom Workshops), pp. 1-6.

7. Duncan MJ, Chan CK, Clarke ND, Cox M, Smith M. The effect of badminton-specific exercise on badminton short-serve performance in competition and practice climates. European Journal of Sport Science, 17(2), pp. 119-126.

8. Hu X, Jiang Q. A study on the assessment and scoring standard of badminton course in colleges and universities: A review. Medicine, 101(49), e32230.

9. Liu H, Leng B, Li Q, Liu Y, Bao D, Cui Y. The effect of eight-week sprint interval training on aerobic performance of elite badminton players. International Journal of Environmental Research and Public Health, 18(2), pp. 638.

10. Williyanto S, Nasuka N, Kusuma DWY. The Development of Badminton Skills Test Instruments for Athletes in Age of Children, Cub, Teenager and Youth. Journal of Physical Education and Sports, 7(1), pp. 50-54.

11. Yüksel MF. A notional analysis in badminton sport: How the hit preferences affect the competition performance. Journal of Athletic Performance and Nutrition, 6(2), pp. 29-43.

12. Krizkova S, Tomaskova H, Tirkolaee EB. Sport performance analysis with a focus on racket sports: A review. Applied Sciences, 11(19), pp. 9212.

13. Torres-Luque G, Blanca-Torres JC, Giménez-Egido JM, Cabello-Manrique D, Ortega-Toro E. Design, validation, and reliability of an observational instrument for technical and tactical actions in singles badminton. Frontiers in Psychology, 11, pp. 582693.

14. Huy CV, Vu NN. Blended learning in badminton training for professionals: Students’ perceptions and performance impacts. European Journal of Physical Education and Sport Science, 6(6).

15. Hambali B, Hidayat Y, Rahmat A. Predictive validity of badminton basic skills learning outcome instrument test based on gender. In 4th International Conference on Sport Science, Health, and Physical Education (ICSSHPE 2019), pp. 373-375. Atlantis Press.

16. Subarjah H, Gilang PP, Sandey TP, Amanda PS. The Effect of Training Motivation and Emotional Intelligence on the Performance of Badminton Players. In International Conference on Education, Science and Technology, pp. 345-352. Redwhite Press.

17. Guo SZ, Mohamad NI, Zakaria J, Yu L, Abd Malek NF. Reliability and Validity of Badminton Special Speed Training Method toward Success Score and Time Perception Predictive Skills Performance of Badminton Players. In Journal of Physics: Conference Series, 1793(1), pp. 012059. IOP Publishing.

18. Zhao W, Wang C, Bi Y, Chen L. Effect of integrative neuromuscular training for injury prevention and sports performance of female badminton players. BioMed Research International, 2021, pp. 1-9.

19. Chiu YL, Tsai CL, Sung WH, Tsai YJ. Feasibility of smartphone-based badminton footwork performance assessment system. Sensors, 20(21), pp. 6035.

20. Kuo KP, Tsai HH, Lin CY, Wu WT. Verification and evaluation of a visual reaction system for badminton training. Sensors, 20(23), pp. 6808.

21. Huang P, Fu L, Zhang Y, Fekete G, Ren F, Gu Y. Biomechanical analysis methods to assess professional badminton players’ lunge performance. JoVE (Journal of Visualized Experiments), 148, pp. e58842.

22. Zheng YJ, Wang WC, Chen YY, Chiu WH, Chen R, Lo CY. Wearable and wireless performance evaluation system for sports science with an example in badminton. Scientific Reports, 12(1), pp. 16855.

23. Yunwei LI, Shiwei J. Video analysis technology and its application in badminton sports training. In Journal of Physics: Conference Series, 1213(2), pp. 022009. IOP Publishing.

24. Sarwar MA, Lin YC, Daraghmi YA, İk TU, Li YL. Skeleton Based Keyframe Detection Framework for Sports Action Analysis: Badminton Smash Case. IEEE Access.

25. Rahmad NA, As’Ari MA, Soeed K, Zulkapri I. Automated badminton smash recognition using convolutional neural network on the vision based data. In IOP Conference Series: Materials Science and Engineering, 884(1), pp. 012009. IOP Publishing. https://www.kaggle.com/code/sidharkal/image-classification-with-yolov8/input

FINANCING

The authors did not receive financing for the development of this research.

CONFLICT OF INTEREST

The authors declare that there is no conflict of interest.

AUTHOR CONTRIBUTION

Conceptualization: Yinghao Li.

Data curation: M N Jawis.

Formal analysis: M N Jawis.

Research: Yinghao Li.

Methodology: Yinghao Li.

Drafting - original draft: Yinghao Li.

Writing - proofreading and editing: M N Jawis.