Category: STEM (Science, Technology, Engineering and Mathematics)
CASE STUDY
Impact of Increasing Albedo on Choosing the Optimal Tilt Angle to Optimize PV Systems: Case Study
Impacto del aumento del Albedo en la Elección del Ángulo de Inclinación Óptimo para Optimizar los Sistemas Fotovoltaicos: Estudio de Caso
Mohsin Ali Diwan1 *, Muhammed Salah Sadiq Al-Kafaji1 *, Ahmed H. Duhis1 *
1Electrical Engineering Techniques Department, Technical College /Al-Mussaib, Al-Furat Al-Awsat Technical University. Iraq.
Cite as: Diwan MA, Sadiq Al-Kafaji MS. Impact of Increasing Albedo on Choosing the Optimal Tilt Angle to Optimize PV Systems : Case Study. Salud, Ciencia y Tecnología - Serie de Conferencias. 2024; 3:863. https://doi.org/10.56294/sctconf2024863
Submitted: 03-02-2024 Revised: 29-04-2024 Accepted: 07-06-2024 Published: 08-06-2024
Editor: Dr.
William Castillo-González ![]()
Note: paper presented at the 3rd Annual International Conference on Information & Sciences (AICIS’23).
ABSTRACT
The amount of irradiation energy that is produced by reflecting one’s surroundings is measured using albedo. The amount of albedo is affected by factors such as time, position, geometry, and meteorological conditions. The albedo value responds to changes in any of the characteristics described above, even if those changes are just slight. Because of this, modelling albedo can be difficult. This paper applied the optimum tilt angle at 31° with a constant albedo 0.2 for location in Al-Furat Al-Awsat Technical University - at latitude 32°03’30.6” North and longitude 44°24’13.3” East. After treating the surface on which the PV system is installed with white Portland cement, the surface albedo will change to (0.87); the increase in albedo leads to an increase in reflected radiation from the ground on PV panels then increase in the power output, also the results shown to reaching the maximum value of the solar irradiation hitting the PV panels to get maximum value of power output with albedo 0.87 in this location, optimum tilt angle will change to be 42o instated of 31o. This study proved that when the albedo of the surface on which the system is installed changes, so does the optimal tilt angle.
Keywords: Albedo; PV Syst.; PV Systems in AL-Kufa City; Optimal Tilt Angle; Albedo Effect.
RESUMEN
La cantidad de energía de irradiación que se produce al reflejar el entorno se mide mediante el albedo. La cantidad de albedo se ve afectada por factores como el tiempo, la posición, la geometría y las condiciones meteorológicas. El valor del albedo responde a cambios en cualquiera de las características descritas anteriormente, aunque esos cambios sean sólo ligeros. Por ello, modelizar el albedo puede resultar difícil. En este trabajo se aplicó el ángulo de inclinación óptimo a 31° con un albedo constante de 0,2 para la ubicación en la Universidad Técnica Al-Furat Al-Awsat, a 32°03’30,6” de latitud norte y 44°24’13,3” de longitud este. Después de tratar la superficie en la que está instalado el sistema fotovoltaico con cemento Portland blanco, el albedo de la superficie cambiará a (0,87); el aumento del albedo conduce a un aumento de la radiación reflejada desde el suelo en los paneles fotovoltaicos y, a continuación, aumenta la producción de energía, también los resultados mostraron que para alcanzar el valor máximo de la irradiación solar que incide en los paneles fotovoltaicos para obtener el valor máximo de producción de energía con albedo 0,87 en esta ubicación, el ángulo de inclinación óptimo cambiará a 42o en lugar de 31o. Este estudio demuestra que cuando el albedo de la superficie sobre la que se instala el sistema cambia, también lo hace el ángulo de inclinación óptimo.
Palabras clave: Albedo; Sistema FV; Sistemas FV en la Ciudad de AL-Kufa; Ángulo de Inclinación Óptimo; Efecto Albedo.
INTRODUCTION
PV Systems: Solar Photovoltaic (PV) systems, often referred to as solar power systems, represent a revolutionary and environmentally friendly approach to harnessing the sun's energy for electricity generation. These systems are designed to convert sunlight directly into electricity, offering a clean and sustainable alternative to traditional fossil fuel-based energy sources. PV systems have gained widespread popularity in recent years due to their numerous benefits, including reduced greenhouse gas emissions, energy independence, and long-term cost savings. They are used in a variety of applications, anywhere from rooftops of houses to huge solar power plants, and play a crucial role in the global transition to cleaner and more sustainable energy sources.(1,2)
The energy output of PV systems is affected by a variety of factors, both environmental and technical. Some of the key factors that can impact on the performance of a PV system are sunlight availability, orientation and tilt angle, temperature, dust and dirt, inverter efficiency, system design, shading and geographical location. Understanding these factors and optimizing the design and maintenance of a PV system can help maximize its energy output and financial benefits. Additionally, advancements in PV technology continue to improve efficiency and overall performance, making solar energy an increasingly viable and sustainable option for electricity generation.(3)
Determining PV panels' optimal tilt angle (OTA)is important because it ensures maximum energy generation. The inclination that is chosen for the photovoltaic panel has an effect on the amount of power that it generates, and the ideal angle is determined by its position. Maintaining an (OTA)of the panel throughout the year is crucial for achieving this goal. The comparative analysis in the studies concludes that optimally placed PV generates 6–7 % more energy than the recommended angles of solar PV systems in the region of study. In addition to maximizing energy generation, determining the (OTA) for PV panels can also lead to cost savings. This is because motor tracking systems, which are often used to adjust a tilt angle of panels, can be expensive. By determining the optimal fixed tilt angle, the need for motor tracking systems can be eliminated, resulting in cost savings.(4,5)
There has been a lot of study done to determine the optimum tilt angle; Jacobson et al.(6) employed a PV watt calculator to estimate the output energy of PV systems based on different tilt angle. In Ozbay et al.(7), different angles have been set manually, and then the current and power are calculated to find the optimal tilt angle. Engineering equation solvers have been used in Ali Morad et al.(8) to make a tilt angle model based on Bernard-Menguy-Schwartz model. In Nfaoui et al.(9), the total amount of solar energy hitting an inclined surface has been calculated using Matlab code and its determined based on the maximum energy absorbed by the solar cells. The global radiation on a solar panel is calculated by Sinha et al.(10) utilising the HOMER software, and then calculating the best tilt angle possible based on Klucher, Davies, Hay and Reindl model.
However, the tilt angle is influenced by many factors. One of these factors is the albedo it's the measure of the reflectivity of a surface. The albedo of the ground surface can affect the (OTA) of the PV panel. In general, the (OTA)of the PV panel is determined based on the direct and diffuse components of solar radiation. However, the albedo of the ground surface can also affect the optimal tilt angle. For example, if the ground surface has a high albedo, it can reflect more solar radiation onto the PV panel, which can increase the PV panel output energy. In this case, the (OTA) may be lower than the angle determined based on direct and diffuse radiation alone. On the other hand, if the ground surface has a low albedo, it can absorb more solar radiation, which can decrease the panel energy output. In this case, the (OTA)may be higher than the angle determined based on direct and diffuse radiation alone.(11) Therefore, this research focuses on the albedo of the ground surface, which should be taken into account when figuring out the (OTA) for the PV system.
Ground-albedo (‘albedo’) is the ratio of ground-reflected irradiation to global irradiation incident to the ground.(12) A dimensionless fraction is measured from 0 to 1. A surface with an albedo of 0 reflects no radiation, while a surface with an albedo of 1 reflects all radiation (mirror and white surface).(13) In the study by Psiloglou et al.(14), surface reflectivity can reach up to 100 W/m2. As a substitute for ground reflected radiation data, 0,2 ground albedo is commonly utilised in PV system modelling. Foreground surfaces might have varying albedos, therefore a constant value is inadequate. The albedo value is very important for PV cells, which gather radiation frontally by catching surface sunlight to generate more energy. Additionally, gloomy skies in northern regions lead to frequent low solar altitudes, making ground reflection a crucial factor in solar energy gain. Further focus will be given later in this article
In most cases, collectors are not positioned horizontally but rather at an angle to maximize the quantity of intercepted radiation while simultaneously minimizing losses due to reflection and cosine. Consequently, those who design systems need information regarding the solar radiation that such surfaces receive, either measured or estimated radiation data.
Solar Irradiation (At) can be expressed at a flat surface absorption of a beam (ABt), diffuse (ADt), and ground reflection (AGt).(15,16)
At= ABt+ ADt+AGt (1)
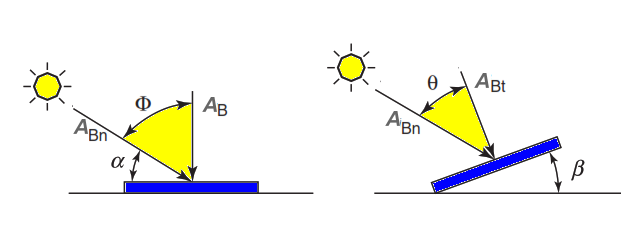
Figure 1. Irradiation of beam on the horizontal and tilted surfaces(17)
Figure 1 illustrates how to express the beam Irradiation of a horizontal surface (AB) and a tilted surface (ABt).
AB= ABn cos (ϕ) (2)
ABt= GBn cos (θ) (3)
The beam Irradiation tile factor for collectors south facing is:
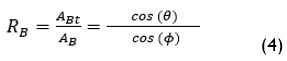
The Irradiation of the beam for any surface is:
ABt=RB AB (5)
The ground-reflected radiation can obtain by ρA (AB + AD), where ρA is the ground albedo.
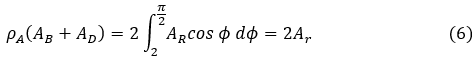
The isotropic ground-reflected radiance is denoted by . (W/m2 rad).
Radiation reflected from the ground on tilted surfaces:
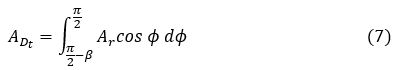
Combining equation (6) and (7) as before:
![]()
Therefore, Substitute equation (7) and (8) into equation (1), get:
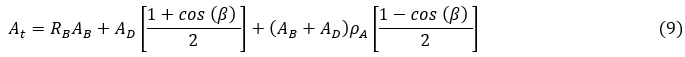
The aggregate radiation received on a flat surface, denoted as (A) G, comprises the summation of the horizontal beam and the diffuse irradiation (18).
![]()
Therefore, equation (9) can be written as:
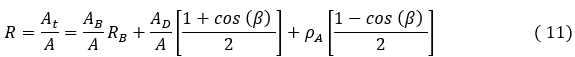
R: tilt factor of total Irradiation
The well-known equation (8) accounts for the albedo contribution to the front surface.(19) Therefore, in PV systems installed on the ground surface to augment the quantity of solar Irradiation received from the ground, it is advisable to select the surface with a higher albedo (ρ).(20)
Developing advanced albedo models is pointless. Assuming a horizontal, finite, and isotropic ground is typical. Thus, the albedo irradiance on an angled surface is:
![]()
Where ρA varies with ground composition. When ρ is unknown, typically ρ = 0,2 is used.
In the simulation method. This database was produce by NASA's Prediction of Worldwide Energy Resource to stimulate renewable energy initiatives by giving public solar radiation and worldwide meteorological data. The NASA SSE database estimates irradiance using 100 km per 100 km zones. Data was obtained between 1983 and 2005. From satellite images, this database calculates daily global, direct, and diffuse irradiance, as well as meteorological variables.(21) Transposing the sun's irradiance falling at a tilted plane into horizontal plane values, like the meteorological database, introduces uncertainty. To calculate the value of diffuse irradiation from a given section of the hemisphere inside the field of vision of a tilted surface, various assumptions must be made.(22) Several authors have analyzed isotropic and anisotropic models in order to discover an accurate data transposition model, which assume that diffuse irradiation is evenly distributed in the same amount and in all directions of the celestial dome.(23) Hay et al.(24) developed a model for forecasting slanted surface diffuse irradiance from horizontal plane data. His transposition factor is made up of two parts. The first examines the isotropic background, while the second examines a circumsolar component that varies inversely with the zenith angle (z) and direct irradiation angle. Hay indexes each model component. Although the Hay model is reliable and used by many photovoltaic system simulation tools, it does not account for the horizon, which contributes to diffuse radiation on an inclined plane. Perez's model took this element into account. Other situations, such as the strengthening of a circumsolar element in atmospheres with a high diffuse irradiation percentage and extreme brightness, were also neglected by the models. In the final model, the clarity index was made independent of the zenith angle in 1990.(25) The equation (12) of the final model expresses diffuse irradiation on a tilted surface.
![]()
Where a and b are a = max (0, cosθ ) , b= max (0,087, cosΦ ), F1 and F2 are horizon/zenith and circumsolar anisotropy coefficients respectively, then:
![]()
On a tilted surface, its global radiation tilt factor is:
![]()
PV syst software includes two transposition modules (Hay and Perez) for calculating global incident in-collector Irradiation (GlobInc) from global horizontal Irradiation (GlobHor). In this study due to its ability to take into account a wider range of astronomical conditions made possible by its higher number of modulating parameters, the Perez transposition modules used to outperform the competition.(26)
The transposition factor (TF) is the ratio of the tilted plane's global irradiation (At) to the horizontal plane's global irradiation (A). In simulation, (GlobInc) is equivalent to (At), while (GlobHor) is equivalent to (A). Because (GlobHor) is constant at any position, the most important parameter in computing (TF) is (GlobInc).
METHOD
PVsyst is a simulation software initially developed in Geneva to facilitate the computation of the performance and functionality of PV systems. As mentioned above, the software simplifies the system configuration process and can compute the quantity of energy produced. The simulation of the sizing system is the basis for the output, with the geographical location of the PV system being the primary determining factor. The outcomes may encompass multiple simulation parameters in monthly, daily, or hourly measurements. The Loss diagram model is utilised to forecast system architecture vulnerabilities, as documented in sources.(27,28) Conducting a simulation in PVSyst involves the following five sequential steps.
Step 1: Selection of the Site
Using google maps as shown in figure 2 to select the locations for solar PV installation for Al-Furat Al-Awsat Technical University located in the Najaf Governorate, the coordinates are 32°03'30,6"N latitude and 44°24'13,0"E longitude, respectively and about 22 meters above sea level. Submit the coordinates in PV Syst. to get the geographical site parameters.

Figure 2. Geographical location Al-Furat Al-Awsat Technical University
Step 2: Choosing the Tilt Angle
From field type on PV Syst. Software fixed tilted plane towards the south choosing the optimization concerning yearly irradiation yield, the tilt angle 31°, and azimuth 0° to get the maximum plane tilt and maximum plane orientation, as shown in figure 3.
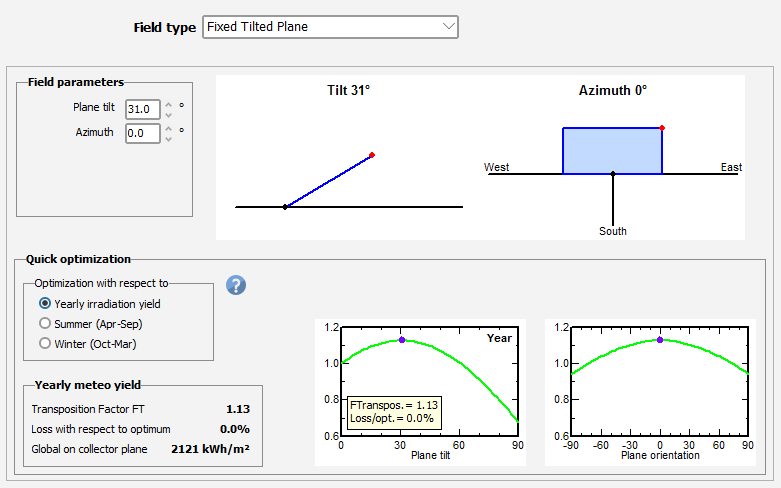
Figure 3. Tilt angle and azimuth of location
Step 3: Daily Consumptions
According to office needed, the load for this simulation contains ( 10 LED lamps, 1 TV , 3 Fan, 1 fridge, 3 Laptop, 3 Printer) the daily power for each load ( 9,80, 65, 2500,80, 120 ) watts, respectively with total daily energy for all loads (8714) Wh/ day and monthly energy (261,4) Kwh/mth as shown in figure 4.
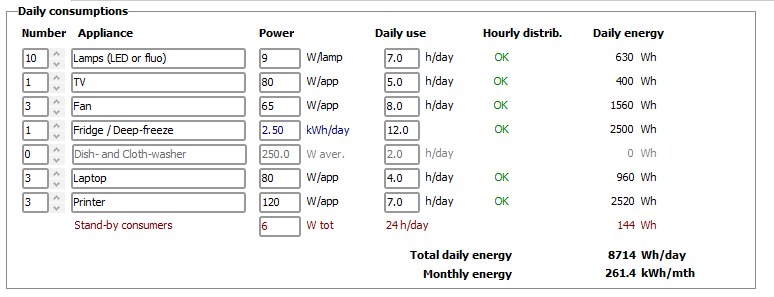
Figure 4. Daily Consumptions for load
Step 4: System Definitions
The stand-alone connected PV system is suitable for Al-Furat Al-Awsat Technical University offices. Figure 5 shows the simulation test elements (2 parallel x4 series) batteries, PV array (4str. of 2 modules) with normal power 2,20 KWp and 1913 normal power universal MPPT controller.
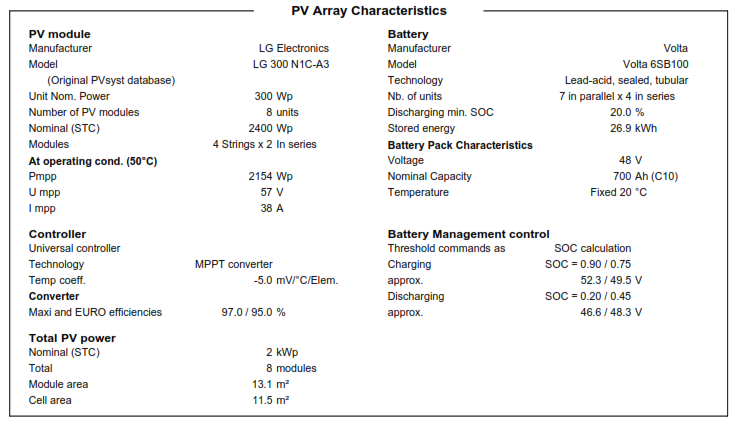
Figure 5. Stand-Alone System Definitions
Step 5: Albedo Setting and tilt angle
Table 1 shows different materials with albedo values.(29,30,31) Utilizing to choose concrete with high solar reflectance. In this study, the comparison will be between constant albedo 0,2. Furthermore, white Portland cement has an albedo of 0,87, as shown in table 6; white Portland cement is a type of cement with a white hue, as its name suggests. The only difference between ordinary grey Portland cement and its counterpart is its color and fineness. The low content of Iron Oxide and Manganese Oxide characterizes the composition of the raw materials used in producing this cement. The oxides impact the brightness and undertone of white Portland cement.
|
Table 1. Different Materials With Albedo Values(31) |
|
|
Concrete constituent |
Albedo |
|
White Portland cement |
0,87 |
|
Ground granulated blast-furnace cement |
0,71–0,75 |
|
Gray Portland cement |
0,32–0,47 |
|
Coal fly ash |
0,28–0,55 |
|
Dark grey riverbed sand (quartz, clay minerals, mica) |
0,20 |
|
Black and red rock (granite) |
0,19 |
|
White rock (plagioclase) |
0,49 |
|
Limestone fine aggregate |
0,42 |
|
Limestone coarse aggregate |
0,42 |
|
Gold and white rock (chert, iron impurities) |
0,55 |
|
Fine grain natural gravel |
0,62 |
In this step, three cases of simulation as described below:
· Case 1: constant albedo (0,2) with optimum tilt angle at this site (31o)
· Case 2: treatment the surface with white Portland cement albedo (0,87). the treatment area will be twice than the area of PV panel(32) the optimum tilt angle at this site (31o).
· Case 3: white Portland Cement albedo (0,87). The tilt angle should increase according to increasing albedo(33) until maximum Irradiation effectively reaches the PV-cell surface, available energy and maximum specific production.
Figure 6 shown how to set the albedo values for three cases.

Figure 6. Set the Albedo Values for Three Cases
RESULTS AND DISCUSSION
This paper examines the impact of various parameters on the combination of (PV) modules as shown in table 2.
|
Table 2. Various Parameters of Simulation |
|
|
Produced Energy |
The basic result of our simulation |
|
Specific Production |
The output energy is divided by the array's nominal power (Pnom at STC). This is a measure of the system's potential, taking into account irradiance conditions (orientation, site location, and meteorological conditions) |
|
GlobInc |
Global Irradiation in the collector plane after transposition, but without any optical corrections |
|
GlobEff |
"Effective" global Irradiation on the collectors, i.e. after optical losses (far and near shadings,IAM, soiling losses). |
|
IAM |
Incidence Angle Modifier |
This section presents a performance analysis of a proposed stand-alone system with batteries with (PV) system power 2200 Wp in three separate cases at Al-Furat Al-Awsat Technical University located in the Najaf Governorate. The coordinates are 32°03'30,6"N latitude and 44°24'13,0"E longitude, respectively and about 22 meters above sea level.
Case 1: 0,2 Albedos with an Optimum Tilt Angle Of 31o
In this case, the constant albedo (0,2) with optimum tilt angle is 31o. As shown in figure 7, this simulation's balances and main results for constant albedo (0,2). The system production is 3591KWh/year; specific production is 1632 KWh/Wp/year.
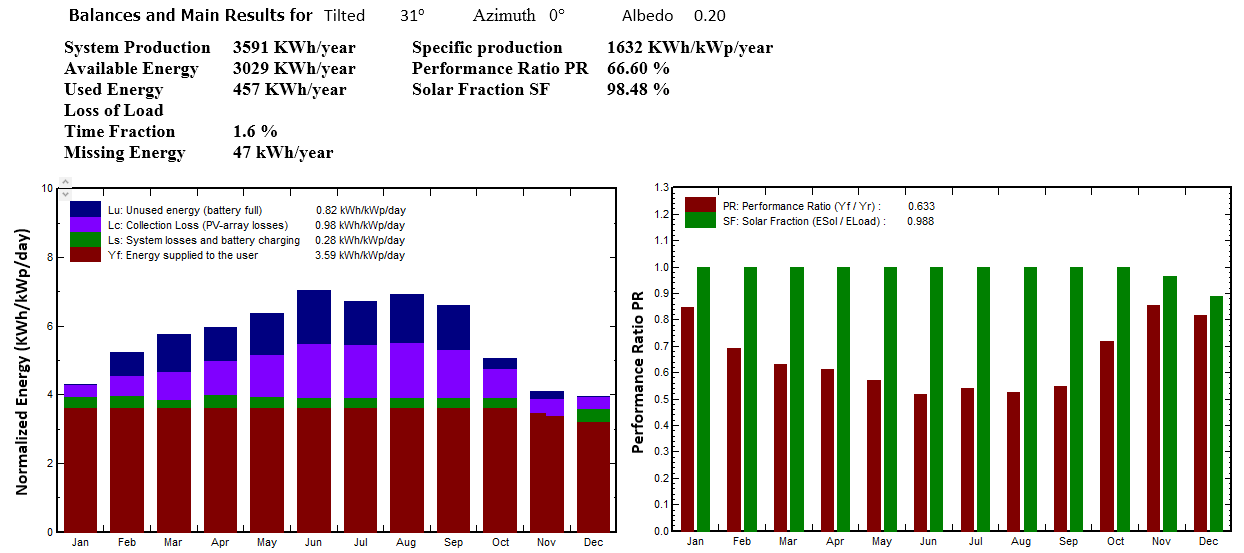
Figure 7. Balances and Main Results with Constant Albedo (0,2) for Case 1
Case 2: 0,87 Albedos with an Optimum Tilt Angle Of 31o
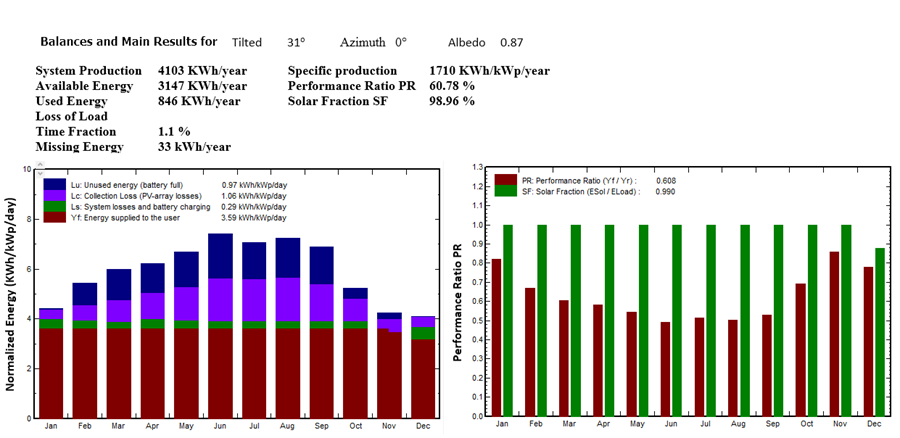
Figure 8. Balances and Main Results with Albedo (0,87) for Case 2
After treatment, the surface of the mounted PV system with white Portland cement with albedo (0,87) with the same optimum tilted angle (31o). Figure 8 shows the balances and main results. The system production is 4103KWh/year; specific production is 1710 KWh/KWp/year.
After comparing the results for case 1 and case 2, the results show that when increasing albedo from 0,2 to 0,87, global Irradiation in the collector plane (GlobInc) will be increased with a percentage from 9,7 % to 14,5 %, then increasing the produced energy from (3960,9 - 4102,9) kWh/year, specific production from (1650-1710) kWh/kWp/year
In addition, as shown in table 3 and figure 9, the other main results related to increased albedo.
|
Table 3. Comparing of Balances and Main Results for Case 1 and Case 2 |
|||||||
|
Case |
Tilt angle |
Albedo |
Global incident in coll. plane |
GlobEff |
Available Energy |
Specific production |
EArray |
|
kWh/m² |
kWh/year |
kWh/kWp/year |
kWh |
||||
|
1 |
31o |
0,20 |
+9,7 % |
2013,9 |
3960,9 |
1650 |
3384,8 |
|
2 |
31o |
0,87 |
+14,5 % |
2097,3 |
4102,9 |
1710 |
3399,7 |
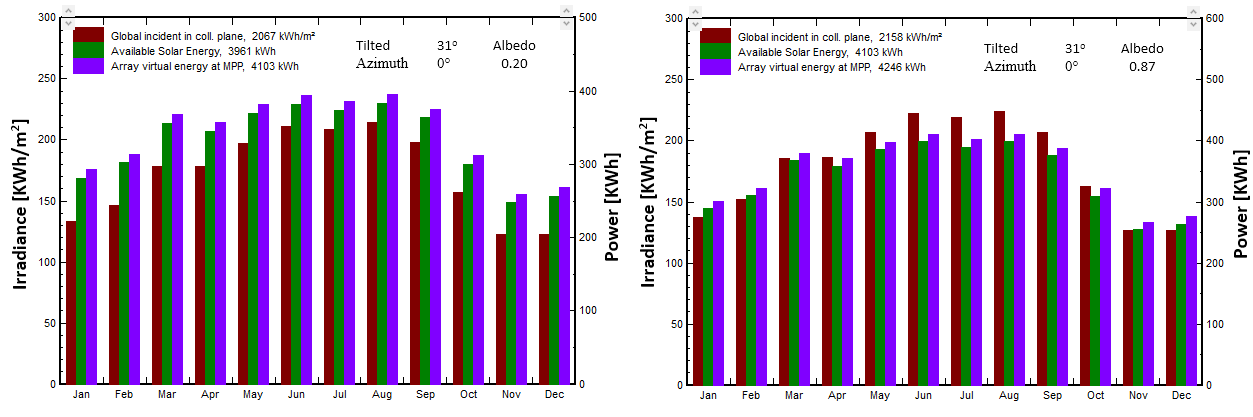
Figure 9. Comparing of Related Results of Increased Albedo for Case1 and Case 2
Case 3: 0,87 Albedo with Different Tilt Angle
The albedo in this case is 0,87. The tilt angle will be increased until it reaches its maximum (GlobInc). The maximum (GlobInc) is (2179,0) kWh/m2 and the greatest output produced energy (4138,7) kWh/year at tilt angle 42o because these features decrease after this angle, as shown in table 4.
|
Table 4. Results of different tilted angles with albedo (0,87) for Case 3 |
|||||||
|
Tilt angle |
GlobHor |
Gain |
GlobInc |
IAM factor on global |
GlobEff |
Alb_Inc |
Available Energy |
|
kWh/m² |
Ratio % |
kWh/m² |
kWh/m² |
kWh/m² |
kWh/year |
||
|
32o |
1883,8 |
1,1473 |
2161,3 |
-2,795 |
2100,9 |
124,50 |
4109,3 |
|
33o |
1883,8 |
1,1491 |
2164,6 |
-2,800 |
2104,0 |
132,20 |
4115,1 |
|
34o |
1883,8 |
1,1507 |
2167,7 |
-2,809 |
2106,8 |
140,09 |
4120,3 |
|
35o |
1883,8 |
1,1521 |
2170,3 |
-2,815 |
2109,2 |
148,19 |
4124,7 |
|
36o |
1883,8 |
1,1533 |
2172,6 |
-2,826 |
2111,2 |
156,50 |
4128,5 |
|
37o |
1883,8 |
1,1544 |
2174,6 |
-2,837 |
2112,9 |
165,00 |
4131,7 |
|
38o |
1883,8 |
1,1552 |
2176,2 |
-2,854 |
2114,1 |
173,71 |
4134,2 |
|
39o |
1883,8 |
1,1559 |
2177,4 |
-2,866 |
2115,0 |
182,61 |
4136,1 |
|
40o |
1883,8 |
1,1563 |
2178,3 |
-2,874 |
2115,7 |
191,71 |
4137,6 |
|
41o |
1883,8 |
1,1566 |
2178,8 |
-2,882 |
2116,0 |
201,00 |
4138,4 |
|
42o |
1883,8 |
1,1567 |
2179,0 |
-2,896 |
2115,9 |
210,48 |
4138,7 |
|
43o |
1883,8 |
1,1566 |
2178,8 |
-2,901 |
2115,6 |
220,14 |
4138,6 |
As shown in table 5 Global horizontal Irradiation (GlobHor) is constant (1883,8) kWh/m². Gain ratio degree, which means the percentage that effect (GlobHor) to reach (GlobInc) and this increases according to the main impact of albedo irradiation in the collector plane because the same effect of changing beam and diffuse irradiance will be constant on the PV panel in this location. IAM is an optical effect (reflection loss) corresponding to the decrease of the Irradiation reaching the PV cells' surface relative to Irradiation under normal incidence. (GlobEff) is obtain by (GlobEff)= (GlobInc) - (GlobInc)* IAM .
Analysis results to choose the optimum tilt angle with maximum (GlobInc) and output produced energy. Table 5 shows the comparison between two angles and the procedure above calculating Irradiation and some major losses of the PV system due to increasing Irradiation on the PV panel at tilt angle (41o, 42o)
|
Table 5. Comparison of Results and Some Major Losses of the PV System between Tilt Angles (41o, 42o) |
||||
|
Variable |
Tilt angle 41o |
Tilt angle 42o |
||
|
Global horizontal Irradiation |
1883,8 kWh/m² |
1883,8 kWh/m² |
||
|
Global incident in coll. plane |
+15,663 % |
2178,8 kWh/m² |
+15,672 % |
2179,0 kWh/m² |
|
IAM factor on global |
-2,885 % |
2116,0 kWh/m² |
-2,894 % |
2115,9 kWh/m² |
|
Effective Irradiation on collectors |
|
2116,0 kWh/m² |
|
2115,9 kWh/m² |
|
Total available Irradiation on an area of 13,1 m² |
|
27761,7 kWh |
|
27761,2 kWh |
|
Array nominal energy (at STC effic.) |
|
5080,2 kWh |
|
5080,1 kWh |
|
PV loss due to irradiance level |
+00,463 % |
5103,7 kWh |
+00,462 % |
5103,6 kWh |
|
PV loss due to temperature |
-12,776 % |
4451,7 kWh |
-12,764 % |
4452,2 kWh |
|
Module quality loss |
0,75 % |
4485 kWh |
0,75 % |
4485,6 kWh |
|
Mismatch loss, modules and strings |
-2,1 % |
4390,9 kWh |
-2,1 % |
4391,4 kWh |
|
Ohmic wiring loss |
-2,455 % |
4283,1 kWh |
-2,455 % |
4283,6 kWh |
|
Unused energy (battery full) |
-20,139 % |
3420,5 kWh |
-20,115 % |
3421,9 kWh |
|
Effective energy at the output of the array |
|
3420,4 kWh |
|
3421,7 kWh |
CONCLUSIONS
This research applies several tilt angles sequentially with variable albedo to get the most effective global Irradiation in the collection plane.
According to the results provided in table 3, with an albedo of (0,2), the optimum tilt angle in this location after testing several angles for getting maximum global Irradiation on the collectors, the greatest produced energy is (31o). The focus of this study is on global Irradiation in the collector plane, which is very important in designing a PV system because incorrect sizing of the PV system causes more losses, which affects not harvesting of the maximum possible output power and makes it difficult to choose the right optimum tilt angle. Increase the tilted angle in table 4 after selecting (0,87) albedo to get maximum global Irradiation in the collection plane; it will be between angles (41o-42o). As shown in table 5, there is three losses effect until obtaining effective energy at the array's output: PV loss due to irradiance level (This is the result of the PV module's low-light efficiency (efficiency concerning efficacy at 1000 W/m2), in tilt angle (41o). It is better; however, the PV loss due to temperature and unused energy (battery full) losses are increase at this tilt angle.
As a result, the tilt angle (42o) is the optimum tilt angle at this location with albedo (0,87). The study fulfilled its objective when the albedo was increased; the optimal tilt angle increased from 31o to 42o, the global Irradiation in the collection plane increased from 2158 kWh/m² to 2179,0 kWh/m² and output produced energy increased from 4102,9 kWh/year to 4138,7 kWh/year.
REFERENCES
1. A. Awasthi et al., "Review on sun tracking technology in solar PV system," Energy Reports, vol. 6, pp. 392-405, 2020/11/01/ 2020.
2. W. Ahmed, J. A. Sheikh, and M. A. P. Mahmud, "Impact of PV System Tracking on Energy Production and Climate Change," Energies, vol. 14, no. 17, p. 5348, 2021.
3. R. J. Mustafa, M. R. Gomaa, M. Al-Dhaifallah, and H. Rezk, "Environmental impacts on the performance of solar photovoltaic systems," Sustainability, vol. 12, no. 2, p. 608, 2020.
4. G. Y. Kim, D. S. Han, and Z. Lee, "Solar Panel Tilt Angle Optimization Using Machine Learning Model: A Case Study of Daegu City, South Korea," Energies, vol. 13, no. 3. doi: 10.3390/en13030529
5. M. K. Sharma, D. Kumar, S. Dhundhara, D. Gaur, and Y. P. Verma, "Optimal tilt angle determination for PV panels using real time data acquisition," Global challenges, vol. 4, no. 8, p. 1900109, 2020.
6. M. Z. Jacobson and V. Jadhav, "World estimates of PV optimal tilt angles and ratios of sunlight incident upon tilted and tracked PV panels relative to horizontal panels," Solar Energy, vol. 169, pp. 55-66, 2018/07/15/ 2018.
7. H. Ozbay, A. Karafil, Y. Onal, M. Kesler, and H. Parmaksiz, "The Monitoring of Monthly, Seasonal and Yearly Optimum Tilt Angles by Raspberry Pi Card for Bilecik City, Turkey," Energy Procedia, vol. 113, pp. 311-318, 2017/05/01/ 2017.
8. A. M. Ali Morad, A. K. Shaker Al-Sayyab, and M. A. Abdulwahid, "Optimisation of tilted angles of a photovoltaic cell to determine the maximum generated electric power: A case study of some Iraqi cities," Case Studies in Thermal Engineering, vol. 12, pp. 484-488, 2018/09/01/ 2018.
9. M. Nfaoui and K. El-Hami, "Optimal tilt angle and orientation for solar photovoltaic arrays: case of Settat city in Morocco," International Journal of Ambient Energy, vol. 41, no. 2, pp. 214-223, 2020.
10. S. Sinha and S. S. Chandel, "Optimum tilt angles for maximum power generation by photovoltaic systems in western himalayan state Of himachal Pradesh, India," in 2016 7th India International Conference on Power Electronics (IICPE), 2016, pp. 1-6.
11. E.-M. Grommes, U. Blieske, and J.-R. Hadji-Minaglou, "Positive Impact of Red Soil on Albedo and the Annual Yield of Bifacial Photovoltaic Systems in Ghana," Energies, vol. 16, no. 4. doi: 10.3390/en16042042
12. B. Y. H. Liu and R. C. Jordan, "The long-term average performance of flat-plate solar-energy collectors: With design data for the U.S., its outlying possessions and Canada," Solar Energy, vol. 7, no. 2, pp. 53-74, 1963/04/01/ 1963.
13. P. Ineichen, O. Guisan, and R. Perez, "Ground-reflected radiation and albedo," Solar Energy, vol. 44, no. 4, pp. 207-214, 1990/01/01/ 1990.
14. B. E. Psiloglou, C. A. Balaras, M. Santamouris, and D. N. Asimakopoulos, "Evaluation of different radiation and albedo models for the prediction of solar radiation incident on tilted surfaces, for four European locations," 1996.
15. A. Z. Hafez, A. Soliman, K. A. El-Metwally, and I. M. Ismail, "Tilt and azimuth angles in solar energy applications – A review," Renewable and Sustainable Energy Reviews, vol. 77, pp. 147-168, 2017/09/01/ 2017.
16. S. A. Kalogirou, Solar energy engineering: processes and systems. Academic press, 2013.
17. A. H. Duhis, M. Aljanabi, and M. S. S. Al-Kafaji, "Increasing photovoltaic system power output with white paint albedo–a scenario in Al-Mausaib City using PVSyst. software," International Journal of Power Electronics and Drive Systems (IJPEDS), vol. 14, no. 2, pp. 1149-1159, 2023.
18. Y.-P. Chang, "An ant direction hybrid differential evolution algorithm in determining the tilt angle for photovoltaic modules," Expert Systems with Applications, vol. 37, no. 7, pp. 5415-5422, 2010/07/01/ 2010.
19. M. A. Mohamed, A. M. Eltamaly, and A. I. Alolah, "Sizing and techno-economic analysis of stand-alone hybrid photovoltaic/wind/diesel/battery power generation systems," Journal of Renewable and Sustainable Energy, vol. 7, no. 6, p. 063128, 2015.
20. U. A. Yusufoglu et al., "Simulation of Energy Production by Bifacial Modules with Revision of Ground Reflection," Energy Procedia, vol. 55, pp. 389-395, 2014/01/01/ 2014.
21. M. K. Da Silva, D. I. Narvaez, K. B. de Melo, T. S. Costa, T. G. de Siqueira, and M. G. Villalva, "Comparative Analysis of Meteorological Databases and Transposition Models Applied To Photovoltaic Systems," vol. 1.
22. J. E. Hay and D. C. McKay, "Estimating solar irradiance on inclined surfaces: a review and assessment of methodologies," International Journal of Solar Energy, vol. 3, no. 4-5, pp. 203-240, 1985.
23. C. A. Gueymard and D. R. Myers, "Solar Radiation Measurement: Progress in Radiometry for Improved Modeling," in Modeling Solar Radiation at the Earth’s Surface: Recent Advances, V. Badescu, Ed. Berlin, Heidelberg: Springer Berlin Heidelberg, 2008, pp. 1-27.
24. J. E. Hay, "Calculation of monthly mean solar radiation for horizontal and inclined surfaces," Solar Energy, vol. 23, no. 4, pp. 301-307, 1979/01/01/ 1979.
25. R. Perez, P. Ineichen, R. Seals, J. Michalsky, and R. Stewart, "Modeling daylight availability and irradiance components from direct and global irradiance," Solar Energy, vol. 44, no. 5, pp. 271-289, 1990/01/01/ 1990.
26. E. Lorenzo, "Energy collected and delivered by PV modules," Handbook of photovoltaic science and engineering, pp. 984-1042, 2011.
27. R. Kumar, C. S. Rajoria, A. Sharma, and S. Suhag, "Design and simulation of standalone solar PV system using PVsyst Software: A case study," Materials Today: Proceedings, vol. 46, pp. 5322-5328, 2021/01/01/ 2021.
28. B. Belmahdi and A. E. Bouardi, "Solar Potential Assessment using PVsyst Software in the Northern Zone of Morocco," Procedia Manufacturing, vol. 46, pp. 738-745, 2020/01/01/ 2020.
29. M. Á. Sanjuán, Á. Morales, and A. Zaragoza, "Precast Concrete Pavements of High Albedo to Achieve the Net “Zero-Emissions” Commitments," Applied Sciences, vol. 12, no. 4, p. 1955, 2022.
30. Y. Kotak, M. S. Gul, T. Muneer, and S. M. Ivanova, "Investigating the impact of ground albedo on the performance of PV systems," 2015.
31. M. Á. Sanjuán, Á. Morales, and A. Zaragoza, "Effect of Precast Concrete Pavement Albedo on the Climate Change Mitigation in Spain," Sustainability, vol. 13, no. 20, p. 11448, 2021.
32. M. Grech, L. Mule Stagno, and C. Yousif, "Increasing PV module output with flat reflectors–a scenario in Malta," 2013.
33. A. Barbón, L. Bayón, G. Díaz, and C. A. Silva, "Investigation of the Effect of Albedo in Photovoltaic Systems for Urban Applications: Case Study for Spain," Energies, vol. 15, no. 21, p. 7905, 2022.
FINANCING
There is no specific funding to support this research.
CONFLICT OF INTEREST
All authors reviewed the results, approved the final version of the manuscript and agreed to publish it.
AUTHORSHIP CONTRIBUTION
Conceptualization: Mohsin Ali Diwan, Muhammed Salah Sadiq Al-Kafaji, Ahmed H. Duhis.
Data curation: Mohsin Ali Diwan, Muhammed Salah Sadiq Al-Kafaji, Ahmed H. Duhis.
Formal analysis: Mohsin Ali Diwan, Muhammed Salah Sadiq Al-Kafaji, Ahmed H. Duhis.
Research: Mohsin Ali Diwan, Muhammed Salah Sadiq Al-Kafaji, Ahmed H. Duhis.
Methodology: Mohsin Ali Diwan, Muhammed Salah Sadiq Al-Kafaji, Ahmed H. Duhis.
Drafting - original draft: Mohsin Ali Diwan, Muhammed Salah Sadiq Al-Kafaji, Ahmed H. Duhis.
Writing - proofreading and editing: Mohsin Ali Diwan, Muhammed Salah Sadiq Al-Kafaji, Ahmed H. Duhis.