Random unbalance response of rotor with CuO Nano Lubricants

doi: 10.56294/sctconf2024826

Categoría: STEM (Science, Technology, Engineering and Mathematics)

ORIGINAL

Random unbalance response of rotor with CuO Nano Lubricants

Respuesta de desequilibrio aleatorio del rotor con nanolubricantes de CuO

Marwan Abdulrazzaq Salman¹ *, Mahmud Rasheed Ismail² *, Hala Salman Hasan¹ *

¹Mechanical Engineering Department, Al-Nahrain University. Al-Jadriyah Bridge, Baghdad, Iraq.

²Prosthetics and Orthotics Engineering Department, Al-Nahrain University. Al-Jadriyah Bridge, Baghdad, Iraq.

Cite as: Salman MA, Rasheed Ismail M, Salman Hasan HS. Random unbalance response of rotor with CuO Nano Lubricants. Salud, Ciencia y Tecnología-Serie de Conferencias. 2024; 3:826. https://doi.org/10.56294/sctconf2024826

Submitted: 21-01-2024 Revised: 04-04-2024 Accepted: 27-05-2024 Published: 28-05-2024

Editor: Dr. William Castillo-González

Note: paper presented at the 3rd Annual International Conference on Information & Sciences (AICIS’23).

ABSTRACT

Random vibration of disc imbalance is a proper simulation model of many practical rotors such as fans, pumps, turbines, generators, and so on. The current investigation examines the consequences of arbitrary stimulation arising from the random imbalance of a rotating disc in the rotor. Such as the force of the air on the turbine fan and misalignment fluctuations in the rotating part, which cause random vibration. Random vibration is a non-deterministic phenomenon, so the specific response cannot be evaluated; rather, statistical methods are suitable. This objective is accomplished by utilizing white noise excitation. Furthermore, the differential of the equation representing the transfer function of the rotor is evaluated since it is essential in the analysis of random vibrations. By converting the physical properties into mathematical models, it becomes possible to examine the random response due to the random excitation of a rotating disc under various influences. Additionally, nanoparticles of copper oxide (CuO) are incorporated into SAE10W-30 oil in order to investigate their effects on random vibration. An analytical solution is used to solve the governing differential equations using MATLAB software, from which the power spectrum density PSD and standard deviation of the response are evaluated. Some experiments are conducted using a rotor model and a random vibration setup. The random excitation is stimulated by white noise. It is found that the best random response occurs in oil lubricant with 0,0527 g of CuO nanoparticles, and the standard deviation of the response is reversely affected by rotor rotation speed. Comparing theoretical and experimental results shows good agreement for evaluating power spectrum density (PSD) and the standard deviation of the response.

Keywords: Rotor Dynamics; Jeffcott Rotor; Random Vibration; Unbalance; Nanoparticle; Copper Oxide; Transfer Function; Gaussian Distribution; Probability.

RESUMEN

La vibración aleatoria del desequilibrio del disco es un modelo de simulación adecuado de muchos rotores prácticos, como ventiladores, bombas, turbinas, generadores, etc. La presente investigación examina las consecuencias de la estimulación arbitraria derivada del desequilibrio aleatorio de un disco giratorio en el rotor. Por ejemplo, la fuerza del aire en el ventilador de la turbina y las fluctuaciones de desalineación en la pieza giratoria, que provocan vibraciones aleatorias. La vibración aleatoria es un fenómeno no determinista, por lo que no puede evaluarse la respuesta específica, sino que son adecuados los métodos estadísticos. Este objetivo se consigue utilizando la excitación de ruido blanco. Además, se evalúa la diferencial de la ecuación que representa la función de transferencia del rotor, ya que es esencial en el análisis de las vibraciones aleatorias. Convirtiendo las propiedades físicas en modelos matemáticos, es posible examinar la respuesta aleatoria debida a la excitación aleatoria de un disco giratorio bajo diversas influencias. Además, se incorporan nanopartículas de óxido de cobre (CuO) al aceite SAE10W-30 para investigar sus efectos sobre las vibraciones aleatorias. Se utiliza una solución analítica para resolver las ecuaciones diferenciales gobernantes mediante el software MATLAB, a partir de la cual se evalúan la densidad del espectro de potencia PSD y la desviación estándar de la respuesta. Se realizan algunos experimentos utilizando un modelo de rotor y una configuración de vibración aleatoria. La excitación aleatoria se estimula mediante ruido blanco. Se observa que la mejor respuesta aleatoria se produce en el lubricante de aceite con 0,0527 g de nanopartículas de CuO, y la desviación estándar de la respuesta se ve afectada inversamente por la velocidad de rotación del rotor. La comparación de los resultados teóricos y experimentales muestra una buena concordancia para evaluar la densidad del espectro de potencia (PSD) y la desviación estándar de la respuesta.

Palabras clave: Dinámica del Rotor; Rotor Jeffcott; Vibración Aleatoria; Desequilibrio; Nanopartícula; Óxido de Cobre; Función de Transferencia; Distribución Gaussiana; Probabilidad.

INTRODUCTION

The field of rotor dynamics, which is an engineering discipline, is concerned with the identification and control of rotor vibrations to ensure that they remain within acceptable limits. This discipline specifically focuses on the study of lateral and torsional vibrations in rotating shafts. Misalignment in stochastic discs can cause significant changes in system behavior and performance, including increased vibration, complex dynamic behavior and uncertainties.^(1,2) Analyzing random vibration on turbine fans or rotor disks is crucial for understanding the rotor components’ behavior, developing predictive models, improving reliability, reducing downtime, and enabling early detection and proactive maintenance.⁽³⁾ The utilization of rotor constituents is evident in both miniature motors and substantial aircraft. Rotors have a wide field of research and an interest in many kinds of vibration and dynamic behavior. However, in the case of random vibration, it is still few. In this regard, Hussien et al.⁽⁴⁾investigated random vibration in order to examine the whirl motion of the Jeffcott rotor. The analysis of the system involved the utilization of kinetic, potential, and dissipation energy. The equations of motion were obtained through the implementation of Lagrangian and Simulink MATLAB software equations. The responses in y and z coordinates were investigated. An examination of the system’s stability was included in the study, revealing stability at 8,000 rpm and a mass ratio of 0,4. J. B. Roberts et al.⁽⁵⁾used the technique of stochastic averaging to address unpredictable vibration problems in rotors. It can handle random excitations and damped systems. Various solutions were explored for different types of vibrations. M. F. Dimentberg et al.⁽⁶⁾proposed two significant impacts of random excitation on a spinning shaft: an increase in the whirl radius and an increase in the non-excited response to rotation speed. They suggested that the findings were useful for evaluating rotor stability online. Dimentberg et al.⁽⁷⁾explored the influence of internal damping on the random oscillations of Jeffcott rotors subjected to random excitations. The findings of this investigation revealed a rise in vibrations as the dynamic instability threshold speed was approached. Furthermore, the analysis of response power spectral densities (PSDs) was conducted to evaluate the coherence function of lateral displacements in two mutually perpendicular directions. Chun-biao Gan et al.⁽⁸⁾applied a Monte Carlo method with a random matrix model to investigate how dispersion parameters and external noise excitation affect the vibrational characteristics of a Jeffcott rotor. The outcomes revealed that increasing disc offset leads to higher critical speeds, and the vibration amplitude has the potential to double. Nicolas Driot et al.⁽⁹⁾employed stochastic techniques to evaluate the stability and steady-state behavior of a skewed Jeffcott rotor. The inherent uncertainty in the geometry introduces random factors that influence internal excitation. The proposed analytical approach offers insights into the likelihood of instability, and the incorporation of stochastic parameters can improve our comprehension of rotating machinery’s susceptibility. In recent years, nanotechnology has attracted great attention in various fields of research due to its distinctive physical and chemical properties.

In the case of using nanoadditives with rotor bearing lubricants, many authors studied their effects on vibration. For example, M. Asrul et al.⁽¹⁰⁾ investigated the effect of adding CuO nanoparticles to engine oil. They found that it can enhance wear and friction attributes, displaying a minimal coefficient of 0,2 % and reaching a peak of 3 %. This alteration resulted in improved tribological characteristics and increased viscosity. M. Asnida et al.⁽¹¹⁾ Scientists employed copper (II) oxide nanoparticles within engine oil to enhance the durability of piston-liner interactions. Their investigation demonstrated that the combination of CuO nanoparticles with SAE10W-30 base oil exhibited remarkable qualities in reducing friction and preventing wear. The most effective conditions for utilizing CuO nanoparticles comprised a concentration of 0,008 %, an operational speed of 291 rpm, and an applied load of 75 152 N. Mohammad et al.⁽¹²⁾ conducted a numerical investigation of simple journal bearings using lubricating oil enhanced with nanoparticles. We examined different nanofluids, such as CuO, TiO2, Ag, and Cu, along with SAE 20W50 as the base fluid. The research findings suggest that the use of nanoparticle-infused lubricants leads to elevated mass coefficients, damping ratios, and improved fluid-effective stiffness. Tariq et al.⁽¹³⁾ examined nanofluid-based lubricating oil that demonstrates the potential to enhance the efficiency of rotating machinery. An analysis was conducted using ANSYS software to assess the influence of nanofluid lubricating oil on fluid film journal bearings. The findings revealed that higher oil fractions led to a 20,4 % and 15,5 % decrease in dynamic response and a corresponding increase in critical speed of 25,82 % and 16,8 %, respectively. The majority of prior studies did not examine the stochastic vibrations affecting the rotor’s supports. Additionally, nano-lubrication was solely employed for journal-bearing simulation within ANSYS.

In the present work, the effect of random vibration due to disc unbalance in the case of using CuO nanoparticles of different weights with bearing lubricant will be investigated. The analysis starts with the basic equation of motion of the rotor. Random vibration is treated via PSD of the excitation of the random excitation and response. The transfer function that describes rotor behavior in the studied case is evaluated. The statistical analysis, including the standard deviation and probability of the random response, is investigated. In order to study the probability of the random vibration response to distinguish the probability of a dangerous region due to a change in the standard deviation according to the Gaussian and Rayleigh, which are familiar in the investigation of random phenomena.

Mathematical Model

Figure 1 depicts the basic rotor model, comprising a flexible rotating shaft with stiffness k, bearing a disc load of mass m, and supported by two journal bearings with stiffness KA and KB and damping CA and CB. The rotations of the shaft introduce two additional damping factors, namely rotating and non-rotating damping (Cr and Cn, respectively).

Figure 1. Jeffcott rotor with one mass on a flexible shaft and bearings that is also flexible

The governing equation of motion of the rotor with a journal bearing and an unbalanced disk is.⁽¹⁴⁾

Disc Unbalance Transfer Function

Assuming zero external forces and the random vibration is due to disc unbalance, equation (1) is reduced to:

The Laplace transform of Equation (2) gives:

To find the frequency response, the above equation is converted to the frequency domain by replacing s with i to get:

Using Cramer’s Rule to find Xc.

The expansion of the dominator gives:

Distribute the multiplication and rearrange the equation by separating the real and imaginary parts.

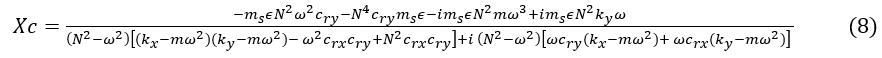
There are two transfer functions for the unbalance in the x and y directions:

Now multiply by the complex conjugate to get:

The real part of equation (10) is:

The imaginary part of equation (10) is:

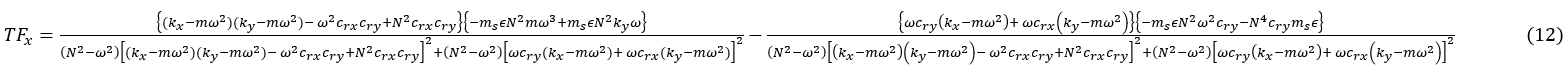
By using Cramer’s Rule and the same procedures, the transfer function in the Y direction is:

Simplifying equation (13) gives:

Distribute the multiplication and re-arrange the equation by separating the real and imaginary parts.

And multiply by the complex conjugate to get:

The real part is:

The imaginary part is:

Random Vibration Analysis

The analysis starts with assessing the autocorrelation of the random signal. The autocorrelation function, denoted as R_xx (τ), is defined as follows:

The power spectral density (PSD) is the Fourier transform of the autocorrelation function.

The random response to the excitation force is simply:

Then the PSD of the response is:

Statistical Analysis of Random Response

In the domain of random vibrations, the concept of temporal averaging over a prolonged period is a recurring idea that is frequently encountered. The prevalent representation for this procedure is established by the subsequent equation x(t), where the variable is denoted;

This number is also equal to the expected value of x(t), which is written as:

The mean square value, designated by the notation ¯(x² )or E[x² (t)] , is found by integrating x² (t) over a time interval T and taking its average value according to the equation:

The variance σ², which is the mean square value about the mean, can be written as:

By expanding the above equation, it is easily seen that:

Experimental work

An experimental rotor setup was created and built for the purpose of validating rotor-dynamic behaviors. The model was used to investigate parameters such as random vibration excitation and the preparation of different concentrations of nanoparticles as lubricant additives.

The experimental set-up includes a rotor supported by two identical and isotropic journal bearings. It is driven by a three-phase AC motor with a variable speed range of 0 to 3360 RPM. The rotor is connected to the motor through a flexible coupling. The AC motor is connected to a variable-frequency drive for controlling the shaft’s angular velocity, as shown in (Figure 2).

Figure 2. The experimental test rig

The schematic drawing of the rotor testing rig is shown in figure 3.

Figure 3. Test schematic drawing of test rig

Figure 4 indicates the complete testing for random vibration due to the unbalance of the rotating disc, including all experimental apparatus.

Figure 4. Complete testing for random vibration due to the unbalance of the rotating disc

The measuring system is divided into two main groups: the input signal and the output signal, as shown in figure 5.

Figure 5. Random vibration analysis

Figure 6 shows a block diagram for the random excitation parts of the instruments.

Figure 6. Excitation side of random vibration

Figure 7 shows a block diagram for the random response parts of the instruments.

Figure 7. Response side of the random vibration

Preparing lubricant with CuO nano-additives

The study investigated the lubrication performance of copper oxide CuO nanoparticles in SAE 10w-30 oil. The nanoparticles, 50 nm in size and spherical, the quantity was determined using a digital weighing apparatus. The nanoparticles were combined with ethylene glycol (C₂H₄(OH)₂) and subjected to an ultrasonic bath for five minutes. This process ensured dispersion and prevented agglomeration of the mixed content, as shown in figure. 8a, b.

Figure 8. (a): Nanoparticles weights (b): ultrasonic bath for samples of lubricants used in Nano for different weights

Viscosity was measured using a rotating spindle inside a Fungilab cup. Rotational viscometers are utilized to determine the viscosity of the sample. Samples were tested with varying rotational speeds, as shown in figure 9.

Figure 9. Rotational viscometer instrument

For every sample of oil, the viscosity was determined, as given in table 1.

Table 1. properties of prepared oil samples
Type of Sample	RPM	Temperature	Viscosity	Density
SAE 10w-30	100	17,5 C°	50,7 mpa.s	909,2 Kg/m³
SAE 10w-30 with 0,0527 g of CuO NP	100	17,5 C°	59,3 mpa.s	911,4 Kg/m³
SAE 10w-30 with 0,2g of CuO NP	100	17,5 C°	56,8 mpa.s	982,8 Kg/m³
SAE 10w-30 with 0,6g of CuO NP	100	17,5 C°	41,7 mpa.s	1055 Kg/m³
SAE 10w-30 with 1 g of CuO NP	100	17,5 C°	47,7 mpa.s	1125,8 Kg/m³

A plot of the viscosity of different nan weights Nanoparticle for two different temperatures is given in figure 10. This figure shows the effect of the CuO nanoparticles as additives to the oil lubricant at different weights. For two different degrees of temperature, both of the curves show that adding a minimum amount of the nanoparticles leads to an increase in viscosity, then the curves begin to drop with increasing the amount of the nanoadditives until they reach 0,6 g, then start to increase quite slightly because of the behavior of nanoparticles at certain concentrations.

Figure 10. Impact of the nanopartical on the viscosity of oil

Four oils were prepared for the supports of the rotor, and then the rotor was operated at a speed of 1 000 rpm. The first sample of oil was used. For the purpose of generating a random vibration on the disc, a white noise generator and a power amplifier were used to move the unbalance mechanism consisting of a solenoid with a mass movement. After that, vibration was transmitted through the accelerometer and signal amplifier to the oscilloscope to view the waves. Then the signal was transferred as an Excel file to the computer so that the signal could be analyzed and the PSD calculated using SIG View. The same experiment was repeated after changing the oil samples.

The SigView program was used to analyze two distinct waves, converting them into Fast Fourier transform FFT and power spectral density PSD formats to determine natural frequency and analyze Gaussian distribution and probability. The research explored rotational speeds and Nano concentrations in relation to journal bearing lubrication.

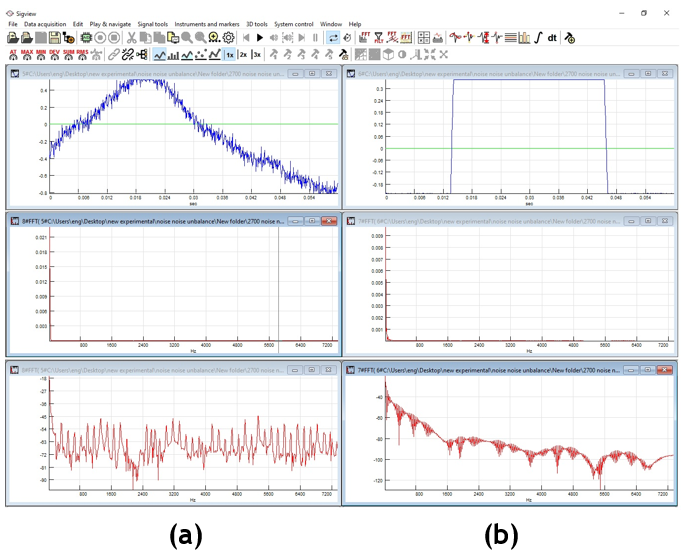
Figure 11. Analysis process of the waves using SigView software: a: excitation, b: response, (a): input signal; (b): output signal

RESULTS AND DISCUSSION

In random vibration the power spectral density (PSD) represent how the power of the response is distributed over a range of frequencies and give the intensity of the effect of random signal on the response, for example in white signal the distribution of the power is constant over all range of frequency of the signal.

Figure 12 shows the relation between the power spectral density response at 1 000 rpm and the frequency from 0-90. For comparison purposes, one case represents the response of pure oil at a viscosity 0,0507 (Pa s.) Inspecting these figures shows that the PSD increases with an increase in frequency, and the largest value of the PSD is found at=0,0417 (Pa s.) in both the x and y directions. The experimental results (blue points) are shown for the four oil samples.

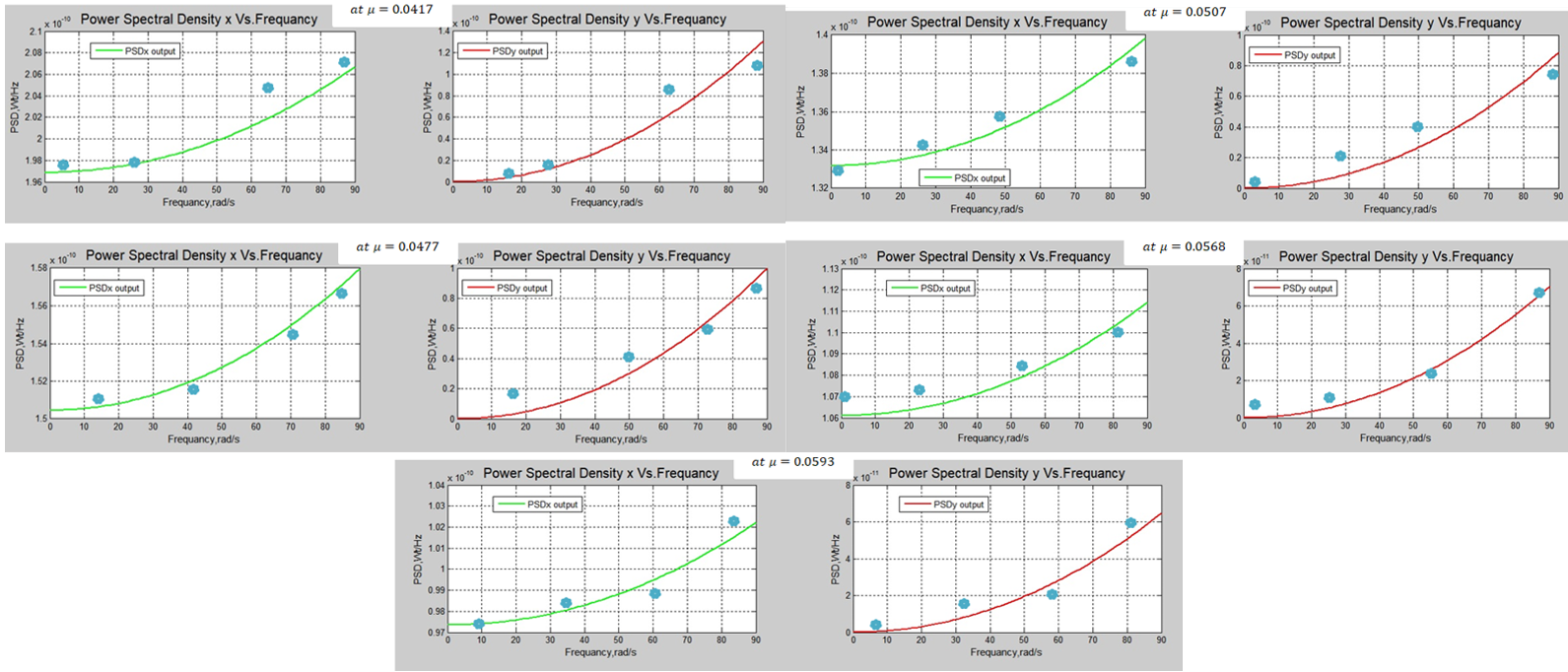
Figure 12. PSD vs. dynamic viscosity for different nanolubricant viscosities in the x and y directions

The relation between the transfer function and the dynamic viscosity is represented in figure 13. In general, the relation gradually decreases with increasing frequency, and the lowest value of the real transfer function in the x-direction for all cases was found at a viscosity of 0,0593 (Pa s.) For the imaginary value of the x-direction and the real value of the y-direction, the lowest value is found at =0,0417 (Pa s.), except for the value of the imaginary transfer function in the y-direction, which increases with increasing frequency, and the highest value for all cases is found at =0,0417( Pa s.)

Figure 13. Transfer function vs dynamic viscosity

Figure 14 shows the relationship between the standard deviation and the dynamic viscosity at different Nano concentrations with a very slight increase with increasing the viscosity of the oil. Assuming the random vibration is of the Gaussian distribution, we found that at σ_x= 2,92755 and σ_y=1,3036 the probability that the response in the x-direction is 68,3 % while at 5,8551, 2,6072 the probability increases to 95,6 % and at 8,78265, 3,9108 for x and y, respectively, the probability will reach to 99,7 % at μ=0,0507 (Pa s). The blue points represent the experimental results.

Figure 14. Standard deviation vs dynamic viscosity

Figure 15 represents the relation between the standard deviation in the x and y directions and the rotational speed from 900 to 3 360 rpm. The highest value of the standard deviation in the x and y directions is at 1 500 rpm, then suddenly starts to decline sharply until it reaches 2 700 rpm. After that, it begins to gradually stabilize horizontally until it reaches the highest rotor speed.

Figure 15. Standard deviation vs rotational speed

Nomenclature

F_n: External force

c_nx=0

c_ny=0

F_x=0

m: Mass of the disc

Ω=N: Spin speed, RPM.

c_n: Rotating damping

c_r: Non-Rotating damping

k_x: Real stiffness coefficient of the bearing in x direction, Ns/m

k_y: Real stiffness coefficient of the bearing in x direction, Ns/m

c_x: Real damping coefficient of the bearing in x direction, Ns/m

c_y: Real damping coefficient of the bearing in y direction, Ns/m

ω: Frequency, rad/s

ω_cr: Critical speed, RPM

CONCLUSIONS

From the dissection of the results, the following conclusions can be derived:

· The derived complex transfer functions proposed mathematical analysis model of a rotor subjected to random vibration due to disc unbalance is suitable for evaluating random responses for different rotor parameters.

· PSD increases with frequency, with the largest value found at lubricant oil with μ=0,0417 (Pa s) Nano additives in both vibration response directions.

· The best Nano-additives for lubricants are 0,0527g of CuO-NP with a viscosity of 0,0593 Pa s, as confirmed by both theoretical and experimental results.

· The standard deviation of response is slightly affected by rotor rotation speed, and the highest value is at velocity equal to 1500rpm.

· For random vibration investigation, the probability of the displacement of the response is specified for both the x and y directions. The maximum probability of the response for the rotor to be safe is 8,78265 in the x direction and 3,9108 in the y direction, respectively.

· In all cases, there is good agreement between the experimental and theoretical PSD random responses.

REFERENCES

1. Li, Z., Jiang, J., & Tian, Z. (2017). Stochastic dynamics of a nonlinear misaligned rotor system subject to random fluid-induced forces. Journal of Computational and Nonlinear Dynamics, 12(1), 011004.

2. Fu, C., Sinou, J. J., Zhu, W., Lu, K., & Yang, Y. (2023). A state-of-the-art review on uncertainty analysis of rotor systems. Mechanical Systems and Signal Processing, 183, 109619.

3. Abdul-Aziz, A., & Woike, M. (2013). Turbine rotor disk health monitoring assessment based on sensor technology and spin tests data. The Scientific World Journal, 2013.

4. Al-Wedyan, H. M., Tahat, M. S., & Mutasher, S. A. (2008). The behaviour of the Jeffcott rotor under a vibrating base of fluid film bearing.

5. Roberts, J. B., & Spanos, P. D. (1986). Stochastic averaging: an approximate method of solving random vibration problems. International Journal of Non-Linear Mechanics, 21(2), 111-134.

6. Dimentberg, M. F., Naess, A., & Sperling, L. (2012). Response of a rotating shaft to uniaxial random excitation.

7. Dimentberg, M. F., Ryzhik, B., & Sperling, L. (2005). Random vibrations of a damped rotating shaft. Journal of Sound and Vibration, 279(1-2), 275-284.

8. Gan, C. B., Wang, Y. H., Yang, S. X., & Cao, Y. L. (2014). Nonparametric modeling and vibration analysis of uncertain Jeffcott rotor with disc offset. International Journal of Mechanical Sciences, 78, 126-134.

9. Driot, N., Berlioz, A., & Lamarque, C. H. (2009). Stability and stationary response of a skew Jeffcott rotor with geometric uncertainty.

10. Asrul, M., Zulkifli, N. W. M., Masjuki, H. H., & Kalam, M. A. (2013). Tribological properties and lubricant mechanism of nanoparticle in engine oil. Procedia Engineering, 68, 320-325.

11. Asnida, M., Hisham, S., Awang, N. W., Amirruddin, A. K., Noor, M. M., Kadirgama, K., & Tarlochan, F. (2018). Copper (II) oxide nanoparticles as additve in engine oil to increase the durability of piston-liner contact. Fuel, 212, 656-667.

12. Jamalabadi, M. Y. A. (2017). Effects of nanoparticle enhanced lubricant films in dynamic properties of plain journal bearings at high Reynolds numbers. Int. J. Eng. Technol, 13, 1-23.

13. Hammza, T. M., Abdulkareem, A. A., & Abas, E. N. (2020). Influence of the Solid Particles Nanofluid on the Dynamic Behaviour of Rotor Fluid Film Journal Bearing Systems. Journal of Mechanical Engineering Research and Developments, CODEN: JERDFO, 43(7), 149.

14. Genta, G. (2005). Dynamics of rotating systems. Springer Science & Business Media.

FINANCING

“The authors did not receive financing for the development of this research”.

CONFLICT OF INTEREST

“The authors declare that there is no conflict of interest”.

AUTHORSHIP CONTRIBUTION

Conceptualization: Marwan Abdulrazzaq Salman, Mahmud Rasheed Ismail, Hala Salman Hasan.

Data curation: Marwan Abdulrazzaq Salman, Mahmud Rasheed Ismail, Hala Salman Hasan.

Formal analysis: Marwan Abdulrazzaq Salman, Mahmud Rasheed Ismail, Hala Salman Hasan.

Research: Marwan Abdulrazzaq Salman, Mahmud Rasheed Ismail, Hala Salman Hasan.

Methodology: Marwan Abdulrazzaq Salman, Mahmud Rasheed Ismail, Hala Salman Hasan.

Drafting - original draft: Marwan Abdulrazzaq Salman, Mahmud Rasheed Ismail, Hala Salman Hasan.

Writing - proofreading and editing: Marwan Abdulrazzaq Salman, Mahmud Rasheed Ismail, Hala Salman Hasan.