Categoría: Education, Teaching, Learning and Assessment
ORIGINAL
An Efficient Hybrid Deep Learning Framework for Predicting Student Academic Performance
Un marco de aprendizaje profundo híbrido eficiente para predecir el rendimiento académico de los estudiantes
M. Viveka1
![]() *, Dr. N.Shanmuga Priya2
*, Dr. N.Shanmuga Priya2
![]() *
*
1Research Scholar (Part Time), Department of Computer Science, Dr. SNS Rajalakshmi College of Arts and Science. Coimbatore – 49.
2Associate Professor & Head, Department of Computer Applications, Dr.SNS Rajalakshmi College of Arts and Science. Coimbatore – 49.
Cite as: Viveka M, Shanmuga Priya D. An Efficient Hybrid Deep Learning Framework for Predicting Student Academic Performance. Salud, Ciencia y Tecnología - Serie de Conferencias. 2024; 3:759. https://doi.org/10.56294/sctconf2024759
Submitted: 28-12-2023 Revised: 17-03-2024 Accepted: 11-05-2024 Published: 12-05-2024
Editor: Dr.
William Castillo-González ![]()
ABSTRACT
Introduction: educational data analysis with data mining techniques for enhanced learning is increasing. Voluminous data available through institutions, online educational resources and virtual educational courses could be useful in tracking learning patterns of students. Data mining techniques could be helpful for predicting students’ academic performance from raw data. Conventional Machine Learning (ML) techniques have so far been widely used for predicting this.
Methods: however, research available on the Convolutional Neural Networks (CNNs) architecture is very scarce in the context of the academic domain. Therefore, in this work a hybrid CNN model involving 2 different CNN models for forecasting academic performance. The one-dimensional data is converted into two-dimensional equivalent to determine efficiency of the hybrid model which is subsequently compared with many existing.
Result: the experimental results are evaluated using various performance metrics like precision, accuracy, recall and F-Score.
Conclusion: the proposed hybrid model outperforms-Nearest Neighbour (K-NN), Decision Trees (DTs), and Artificial Neural Network (ANN) in terms of precision, accuracy, recall and F-Score.
Keywords: Student, Academic Performance; Educational Data Mining (EDM); Convolutional Neural Networks (CNNs).
RESUMEN
Introducción: el análisis de datos educativos con técnicas de minería de datos para mejorar el aprendizaje está aumentando. La gran cantidad de datos disponibles a través de instituciones, recursos educativos en línea y cursos educativos virtuales podrían ser útiles para rastrear los patrones de aprendizaje de los estudiantes. Las técnicas de minería de datos podrían resultar útiles para predecir el rendimiento académico de los estudiantes a partir de datos sin procesar. Hasta ahora, las técnicas convencionales de aprendizaje automático (ML) se han utilizado ampliamente para predecir esto.
Métodos: sin embargo, la investigación disponible sobre la arquitectura de redes neuronales convolucionales (CNN) es muy escasa en el contexto del dominio académico. Por lo tanto, en este trabajo se utiliza un modelo CNN híbrido que involucra 2 modelos CNN diferentes para pronosticar el rendimiento académico. Los datos unidimensionales se convierten en equivalentes bidimensionales para determinar la eficiencia del modelo híbrido que posteriormente se compara con muchos existentes.
Resultado: los resultados experimentales se evalúan utilizando varias métricas de rendimiento como precisión, exactitud, recuperación y F-Score.
Conclusión: el modelo híbrido propuesto supera al vecino más cercano (K-NN), los árboles de decisión (DT) y la red neuronal artificial (ANN) en términos de precisión, exactitud, recuperación y puntuación F.
Palabras clave: Estudiante; Rendimiento Académico; Minería de Datos Educativos (EDM); Redes Neuronales Convolucionales (CNN).
INTRODUCTION
Every student is an asset to educational institutions, as they want them to excel academically.(1) Good academic grades help students secure admissions in prestigious institutions and find high paid jobs. Grade Point Average (GPA) of high school students determine the college they will enter and their financial prospects.(2) Data mining could be utilized to forecast students' performance by analysing the available data.(3,4)
Extraction of information from large amount of raw data could be applied in areas like stock markets, manufacturing, engineering, healthcare, bioinformatics, remote sensing, business and fraud detection in addition to educational sector.(5,6) Because of the increasing trend in the usage of VR systems, ipads, tablets, laptops and mobiles among the students, data acquisition has become easier. Educational Data Mining (EDM) is very useful in extracting information from the unprocessed data available in educational institutions.(7) EDM is capable of extracting hidden information in the raw data. This helps in the prediction of pass or fail rate of students precisely.
Student-related data are of great interest to researchers as they could be utilized to forecast students' performance of students, percentage of dropouts, finding deviations in student actions and examining their activities psychologically.(8,9) By making suitable predictions, the performance of student may be improved by enabling the teachers, parents as well as students themselves to get involved in remedial actions.(10)
This research work focuses on improving students’ academic performance which is impacted by demographics, psychological, personal, educational background as well as environmental impacts. By using data mining, EDM(11,12) helps in finding the association amid parameters and academic performance of student. Student information includes features related to assessment, personal, registration etc.,Convolutional Neural Network (CNN) determines hidden layer features automatically, eliminating distinct feature extractions as seen in traditional ML methods. CNN is used in image classification as well as object detection.A hybrid model including 2 separate CNN models involving 2D data is used for forecasting performances of students. The efficiency of the suggestedtechnique is compared K-Nearest Neighbour (KNN), Decision Tree (DT) and Artificial Neural Network (ANN) to compare performance of model based on precision,accuracy, recall and F-Score.
In this paper, numerical one dimensional data is converted to its corresponding two dimensional form for hybrid model’s utilization which are used in EDM by combining dual CNN models. The efficiency of the suggested techniqueis analysed and compared with standard models. Due to CNN's effective processing, one-dimensional numerical data is transformed into two-dimensional data. In the EDM domain, a hybrid CNN model is produced using CNN models with varying counts of convolution and pooling layers.
The sections are organised as discussed below. Section 2 gives a detailed view of work done by various authors related to student performance analysis. Section 3 gives an overview of existing models. The suggested structure is fully described in Section 4. In Section 5, the results are explained, while Section 6 explains the conclusion.
Related work
Here, the existing works related to student academic performance are detailed.
Helal et al.(13) conducted a study that produced diverse classification models for envisaging performances of students based on the data gathered from Australian university which includes details related to student enrolments, activity data from Learning Management System (LMS). Student heterogeneity is considered in building predictive models. Students with various socio-demographic traits or learning preferences will draw motivation for learning from various sources. The identification of vulnerable pupils is more precise. No approach outperforms others in all categories, according to studies.
In the study by Francis et al.(14), a prediction algorithm is designed for assessing student’s academic performance based on classification as well as clustering schemes. The scheme is analysed with diverse student datasets of several academic disciplines of educational institutions in Kerala, India. It is seen that features related to academics, behaviour, demographics etc. Are taken for analysis. It is seen that the hybrid scheme offers improved accuracy related to academic performance.
Beaulac et al.(15) have built 2 classifiers using Random Forests (RFs). First 2 semesters are used for predicting and determining whether they are eligible for getting an undergraduate degree. The major of a student who has finished a program is determined using few initial courses they have registered. Classification tree is an instinctive and dominant classifier, and constructing a RF develops this classifier. RFs permit reliable measurements which detail which variables can be useful to classifiers and may be used for understanding what is statistically linked to students’ states. They offer useful information for university administrations.
Tsiakmaki et al(16) have examined the efficacy of Transfer Learning (TL) from Deep Neural Networks (DNNs) for forecasting student performances in higher education. Building predictive models in EDM using TL methods are not extensively studied. Hence, several experiments were conducted using data from 5 mandatory courses of 2 undergraduate programs. The scheme enables accurate prediction of students who tend to fail, given that student datasets of who have taken up other associated courses are accessible.
It is essential to control factors that have an impact on how the material is learned. A collection of machine learning techniques were applied by Rivas et al.(17) on a publicly available dataset made up of tree models with various ANN kinds. The frequency with which students use the VLE's materials is thought to have an impact on how well they achieve. At the University of Salamanca, 120 master's degree candidates in computer engineering participated in this study.
Yousafzai et al.(18) examined attention-based Bidirectional LSTM (BiLSTM), a Deep Neural Network (DNN) model, to proficiently envisage performances of students from past data. BiLSTM is linked with attention scheme model by examining present research issues that are constructed on advanced feature classification as well as prediction. The superior sequence learning abilities of the proposed scheme offers improved performance in contrast to standard schemes.
Dabhade et al.(19) presented a study that entailed assessing the results of student learning. The institution's academic department and a questionnaire-based survey were used to create a data collection. To eliminate dimensionality from the data and retrieve the majority of the important characteristics, the data is pre-processed before factor analysis is applied to the resulting data set. To create better predictions, the linear support vector regression approach is applied.
Baashar et al.(20) have examined and surveyed literature related to ANN schemes used in forecasting students’ academic performance especially higher education. ANNs can combine data analyses and data mining schemes for evaluating results of educational achievements. Patterns were not identified concerning selection of input variables as they are based on study and data availability.
Existing models
In this section, the details of some of the existing models(21) to classify data are detailed.
K-Nearest Neighbour (KNN)
K-Nearest Neighbour (K-NN) is a basic but vital Supervised Learning (SL)-based classification algorithm. It finds its application in several areas like pattern identification, data mining as well as intrusion detection. No distribution of data assumptions is made. With training data, coordinates are classified into groups found by a feature. The majority class label defines the label of a data point amid nearest ‘k’ neighbours in feature space.(22)
Efficient choice of ‘K’ while building the model plays a dominant role. Choosing an optimal value for ‘K’ is challenging. Smaller value means that noise has greater influence on the outcome. This leads to increased probability of overfitting. A larger value makes it computationally costly as it involves more time for building the model. Larger value will support smoother decision boundary offering reduced variance but increased bias. An odd value of ‘K’ is advisable for even number of classes. Elbow method can be applied to choose the value of ‘K’. Results may be optimised using Cross Validation scheme.
Decision Tree (DT)
Decision Tree (DT) is a SL method which is non-parametric. It plays a dominant role in classification and regression. It aids in predicting predicts target variable’s value by learning decision rules determined from features.(23) The internal nodes represent attributes, branches show decisions or collection of rules, whereas leaves indicate output. Leaves offer outputs of judgments and do not facilitate any branching, whereas nodes are involved in making judgments. The decisions are taken based on features of given database. It involves questions and separates trees into respective sub-trees depending on response that is yes or no. DTs imitate human thinking abilities while making choices, enabling them to be simple in interpretation.
Artificial Neural Network (ANN)
ANN(24) involves artificial neurons called units which are organised as a sequence of layers which establish whole ANNs. They mimic a network of neurons in human brain enabling systems to comprehend things and take decisions like humans. The layers may have varying number of units based on the system complexity. The network has an input, output and hidden layers. Data which has to be analysed is fed to input layers and it passes through many hidden layers which transform inputs compatible for output layers which offer responses to given inputs.
Units are interconnected between layers. These connections come with weights which find the impact of one on another unit. As data moves from a unit to another, the Neural Network (NN) learns about data that results in output at the output layer. They are trained using training sets. ANN is used for classifying data and the output obtained is validated by human-generated description. In case classification is incorrectly done, back-propagation is applied to regulate whatever is learnt while training. It fine-tunes the connection weights in ANN units depending on obtained error rate. This continues until the network recognizes an image or data with reduced amount of error rates.
Enhanced cnn-based model
Here, the details of the dataset used, data pre-processing and representation and the process of classification using hybrid model is presented (Figure 1).
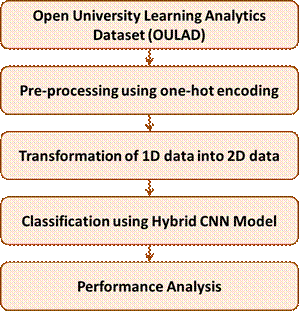
Figure 1. Proposed Model
Dataset
Open University Learning Analytics Dataset (OULAD) is used in this research(25) It includes data of 32 593 students studying in 22 Open University courses during 2013 and 2014. The database includes 7 diverse files. Data on the modules taught are included in the course file. The assessment file includes data associated with various assessments for every module. Virtual Learning Environment (VLE) file includes data about materials in VLE.
· Student info: Contains data related to student demographics.
· Student Registration: Includes in formation associated with students registered/unregistered for courses.
· Student Assessment: Includes assessment results.
· Student Vle: Includes information associated with the student’s involvement in VLE materials.
The above provided files are processed to make the dataset ready.
Data Pre-processing
The 7 files are processed using Python platform and a single .csv file including demographic information, assessments, final results and day-to-day interactions with university VLE are produced. Around 3024 records were under distinction, 12 361 represented pass cases, while 7 052 shown fail and 10 156 records signified withdrawn cases. To support binary classification, first 2 and second 2 cases are combined. Categorical variables are converted to numbers saved in datasets by applying one-hot encoding on categorical variables.
Data Representation
Once encoding is done, the dataset with records of 32 593 students is obtained. AhybridCNN model is used in this work. The data given as input is in 1D format which is to be transformed to 2D that is appropriate for proposedframework. Once categorical values are modified to numerical ones, around 35 numerical features are identified. Every row is based on the number of features. To transform into 2D, zero padding is done for increasing the number of features to 40. A 2D matrix of size 8x5x1 is constructed. Once zero padding is done, reshaping is done such that every array of size 40 is transformed to 8x5x1 size matrix. The 2D representations of 32 593 students are obtained.
Proposed CNN-based Model
Initially, the dataset to be used (OULAD) is decided. Secondly, the data is pre-processed. Then the 1D data is converted to 2D form. A hybrid CNN model is built. Student performance is predicted which includes pass or fail. Lastly, performance is compared with some baseline models.
Two dissimilar CNNs with varying number of layers is proposed. Assume that 1 has 6 layers and the other 5 layers before dense layers.
A layer of input serves as the model's foundation, and it has the dimensions RC1. The open convolutional layer of the first model is then given the input. A group of characteristics are defined by this class. A feature map is produced by applying the filter to the 2D data and then convolves with inputs. There are several hyper-parameters for this class. It is specified how many filters there will be, their sizes, and the stages at which they will be drawn on the 2D data. The outputs of classes range from (1) to (3).
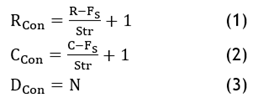
Where:
Str- Stride step
N - Number of filters
-Filter size
R - Row of 2D data
C – Column of 2D data
In case if Str=1, then filters are moved pixel by pixel. This layer has 64 filters of size 3x3 with ‘Fs’ ‘one’. The output is of size 6×3×64.
The pooling layer is the next layer. It drops the size of input without dropping any information. For size reduction either average pooling or max pooling are applied. Pooling is achieved with 2x2 patches with stride 2. Thepooling layer’s output is given below.
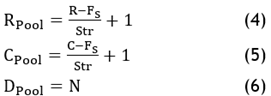
Max pooling applied on input for initial pooling layer 6x3x64. The output is 3x1x64 with ‘Fs’ of 2. The next layer is again a convolution layer with 32 filters of size 1x1. The output is of size 3x1x32.
The next layer is another convolutional layer with 8x1x1 filters. The output is of size 3x1x8.
The feature map is sent to next layer, where flattening is performed on input to convert it into one layer 1D vector of size 24. This is sent to fully connected layer.
The input 8x5x1 2D input is employed to convolutional layer, with 32 filters of size 3x3 and a ‘Fs’ of 1. The feature map of second layer is of size 6x3x32 . The max-pooling layer is of size of 2x2. Output of next layer is 3x1x32. The fourth layer is a convolution layer, the output of size 3x1x32 and next layer is the flattening layer that offers lengthier 1D vector of length 24.
The models are concatenated and output of concatenating layer includes a vector of length 48 is sent to fully connected layers where dual dense layers are used. A dense layer involves neurons on input side connected to those on the output side.
The dense layer offers an output of 1D vector of size 8. Eight input neurons and two output neurons make up the last dense layer. The eventual outcome is compared to the initial label to ascertain how well the forecast was made.
The input signal's non-linear transformation is supported by the activation function. The model's dense initial layer and convolution layers both employ ReLU. The formula is as y = max(0,x). It changes negative feature map values to 0 (zero). The input signal is given nonlinearity in the last dense layer via sigmoid activation function.
The learning algorithm of hybrid CNN is listed below.
· Reform every input into 2D to get an input of size R x C x D.
· Convolutional Layer: Define ‘N’, ‘Fs’ and ‘Str’ and determine the feature map of size of RCon X CCon X DCon (Eqns (1) to (3)).
· Pooling Layer: Feature map (RCon X CCon X DCon) is given as input. Define ‘’ and ‘’ and determine output of size of RPool X CPool X DPool (Eqns (4) to (6)).
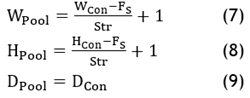
· Convolutional layer: Define ‘’, ‘’ and ‘’ and determine the feature map of size of RCon2 X CCon2 X DCon2, where:

· Convolutional Layer: Define ‘N’, ‘Fs’ and ‘Srt’ and determine the feature map of size of RCon3 X CCon3 X DCon3,where:
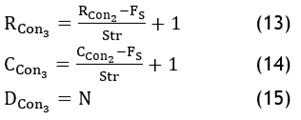
· Flattened layer: Transform output of previous step to single-layer 1D vector
· Convolutional layer: Input is of size. Determine feature map with size of RCon4 X CCon4 X DCon4, where:
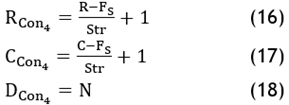
· Pooling layer: Define ‘Fs’ and ‘Str’ and determine the output of size of RPool2 X CPool2 X DPool2,where:
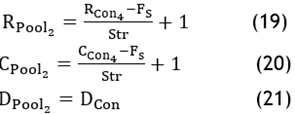
· Convolutional layer: Define ‘N’, ‘Fs’ and ‘Str’ and determine the feature map of size of RCon5 X CCon5 X DCon5,where:
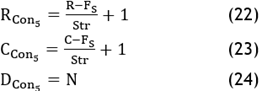
· Flattened layer: Convert output of previous step to single-layer 1D vector.
· Fully-connected layer: Concatenate output from first flattened layer and fifth convolutional layer to generate 1D long vector and give as input to this layer.
· Dense layer: Define input and output neurons and pass outputs to subsequent dense layers.
· Dense layer: Define neuron outputs as counts of classes in dataset.
· Predict label and compute accuracy.
Results and Discussion
The dataset is divided into training test (70 %) and test set (30 %). Test data is used as validation data. Test losses as well as test accuracies imply validation losses as well as accuracies correspondingly. Parameter tuning is utilized to get better results.
Learning rate is considered to be in the range of 0 - 1 which is utilized in training data. It is used in controlling how fast model can adapt to the issue. Increased learning rate leads to rapidly converge to alow quality solution, whereas a low value leads the process in getting stuck. Increased accuracy is obtained at a learning rate of 0,01.
The following formulae are used tocalculate performance indicators including values of precision, recall, F-scores, and accuracies:
Precisions are ratios of successfully recognised positive observations to total anticipated positive observations and computed using.
![]()
Proportions of properly detected positive observations to all observations called sensitivity and computed using:
![]()
Weighed averages of accuracies and recalls yield F1 scores where false positives and negatives are accepted and accuracy computed using positive and negative values:
![]()
Accuracy is calculated in terms of positives and negatives as follows:
![]()
Learning curve becomes flat for increased learning rates. The model is not capable of learning at increased learning rate. Test loss and test accuracy are displayed in table 1 for varying learning rates.
|
Table 1. Test Loss and Test Accuracy for Varying Learning Rates |
||
|
Learning Rate |
Test Loss |
Test Accuracy |
|
1 |
7,23 |
56 |
|
1x 10-1 |
1,67 |
67 |
|
1 x 10-2 |
0,98 |
79 |
|
1 x 10-3 |
0,74 |
93,5 |
|
1 x 10-4 |
0,52 |
83 |
Different number of epochs is used for determining accuracy of model. Test losses and test accuracies are displayed in table 2 for varying number of epochs.
|
Table 2. Test loss and Test Accuracy for Varying Number of Epochs |
||
|
Number of Epochs |
Test Loss |
Test Accuracy |
|
20 |
0,49 |
78 |
|
50 |
0,37 |
83 |
|
100 |
0,35 |
87 |
|
200 |
0,29 |
89 |
|
400 |
0,29 |
88 |
|
600 |
0,28 |
88 |
An increased Accuracy of 89 % is obtained for 200 epochs. Test loss increased with the number of epochs due to over fitting. As the test loss starts increasing, it is advisable to stop training. This is known as early stopping criteria.
The model's effectiveness is contrasted with existing models which include KNN, DT and ANN. KNN, ANN and DT offers 14,7 %, 10,7 % and 3,9 % lesser Accuracy in contrast to the proposed Hybrid CNN model (Figure 2).
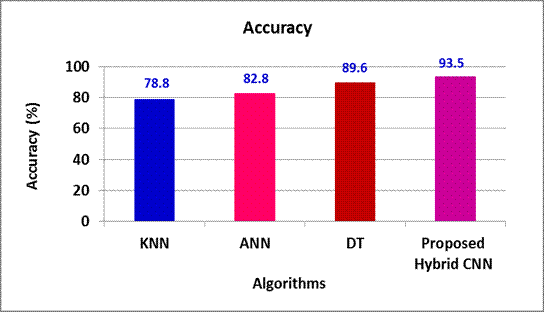
Figure 2. Accuracy
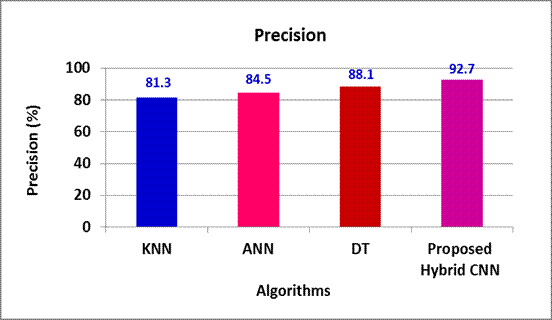
Figure 3. Precision
KNN, ANN and DT offers 11,4 %, 8,2 % and 4,6 % reduced Precision in contrast to the proposed Hybrid CNN model (Figure 3).
KNN, ANN and DT offers 17 %, 11 % and 7,3 % lesser Recall in contrast to the proposed Hybrid CNN model (Figure 4).
KNN, ANN and DT offers 15 %, 10,8 % and 5,7 % reduced F-Score in contrast to the proposed Hybrid CNN model (Figure 5).
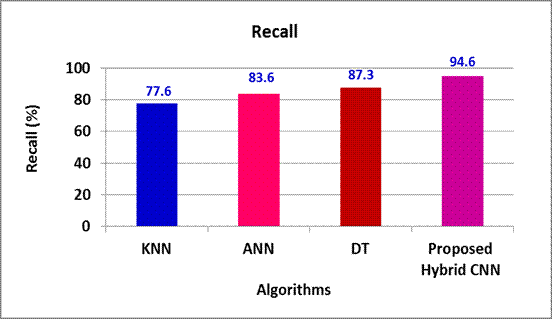
Figure 4. Recall
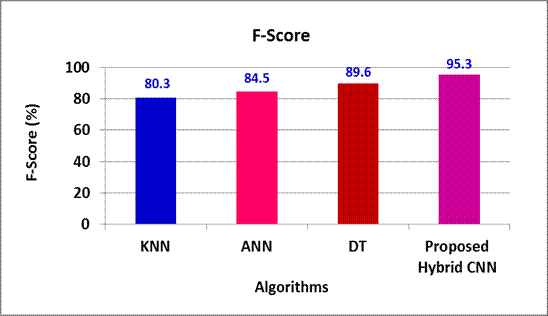
Figure 5. F-Score
CONCLUSION
Deep learning-based methods are used for predicting student academic performance using OULAD dataset. 1D data was converted to 2D data by reshaping data using 40 features. A hybrid model was built using 2 CNNs with varying convolutional and pooling sizes. Performance is evaluated against reference models. Different learning rates were used, and a learning rate of 0,001 resulted in the greatest accuracy. The proposed model is 93,5 % accurate. EDM aids in the extraction of hidden information from raw data as well as the analysis and prediction of student success. The hybrid CNN framework that has been presented can forecast whether a pupil will succeed or fail. To ensure that EDM can learn, the suggested model may be used with big picture data sets. We will be able to observe how our approach impacts other performance indicators, such as kappa, sensitivity, etc. in the future. In this study, we did not look at how individual traits affect academic success; however, this is something we intend to do in the future. Explainable AI is an intriguing subject that may be tackled in the future, despite the limited size of our data collection. Smaller data sets are most suited for explainable AI. The current study illustrates how educational institutions may utilise CNN architecture to forecast student learning results and implement sensible student assistance measures.
REFERENCES
1. Kaunang FJ, and Rotikan R. Students' academic performance prediction using data mining. In Third International Conference on Informatics and Computing (ICIC), pp. 1-5. https://doi.org/10.1109/IAC.2018.8780547.
2. Saravanan V, and Shanmuga Priya N. Feature Detection and Extraction Techniques for Real‐Time Student Monitoring in Sensor Data Environments. Sensor Data Analysis and Management: The Role of Deep Learning, pp. 97-102. https://doi.org/10.1002/9781119682806.ch5.
3. Ha DT, Loan PTT, Giap CN, and Huong NTL. An empirical study for student academic performance prediction using machine learning techniques. International Journal of Computer Science and Information Security (IJCSIS), 18(3), pp. 75-82.
4. Asiah M, Zulkarnaen KN, Safaai D, Hafzan MYNN, Saberi MM, and Syuhaida SS. A review on predictive modeling technique for student academic performance monitoring. In MATEC Web of Conferences, 255, pp. 1-8. https://doi.org/10.1051/matecconf/201925503004.
5. Nuankaew W, and Thongkam J. Improving student academic performance prediction models using feature selection. In 17th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), pp. 392-395. https://doi.org/10.1109/ECTI-CON49241.2020.9158286.
6. Li X, Zhu X, Zhu X, Ji Y, and Tang X. Student academic performance prediction using deep multi-source behavior sequential network. In Advances in Knowledge Discovery and Data Mining: 24th Pacific-Asia Conference, PAKDD, Proceedings, Part I 24, pp. 567-579. https://doi.org/10.1007/978-3-030-47426-3_44.
7. Lu OH, Huang AY, Huang JC, Lin AJ, Ogata H, and Yang SJ. Applying learning analytics for the early prediction of Students' academic performance in blended learning. Journal of Educational Technology & Society, 21(2), pp. 220-232.
8. Jiao P, Ouyang F, Zhang Q, and Alavi AH. Artificial intelligence-enabled prediction model of student academic performance in online engineering education. Artificial Intelligence Review, 55(8), pp. 6321-6344. https://doi.org/10.1007/s10462-022-10155-y.
9. Huang S, and Fang N. Predicting student academic performance in an engineering dynamics course: A comparison of four types of predictive mathematical models. Computers & Education, 61, pp. 133-145. https://doi.org/10.1016/j.compedu.2012.08.015.
10. Nabil A, Seyam M, and Abou-Elfetouh A. Prediction of students’ academic performance based on courses’ grades using deep neural networks. IEEE Access, 9, pp. 140731-140746. https://doi.org/10.1109/ACCESS.2021.3119596.
11. Kamal P, and Ahuja S. Academic performance prediction using data mining techniques: Identification of influential factors effecting the academic performance in undergrad professional course. In Harmony Search and Nature Inspired Optimization Algorithms: Theory and Applications, ICHSA, pp. 835-843. https://doi.org/10.1007/978-981-13-0761-4_79.
12. Rebai S, Yahia FB, and Essid H. A graphically based machine learning approach to predict secondary schools performance in Tunisia. Socio-Economic Planning Sciences, 70, pp. 100724. https://doi.org/10.1016/j.seps.2019.06.009.
13. Trakunphutthirak R, and Lee VC. Application of educational data mining approach for student academic performance prediction using progressive temporal data. Journal of Educational Computing Research, 60(3), pp. 742-776. https://doi.org/10.1177/07356331211048777.
14. Helal S, Li J, Liu L, Ebrahimie E, Dawson S, Murray DJ, and Long Q. Predicting academic performance by considering student heterogeneity. Knowledge-Based Systems, 161, pp. 134-146. https://doi.org/10.1016/j.knosys.2018.07.042.
15. Francis BK, and Babu SS. Predicting academic performance of students using a hybrid data mining approach. Journal of medical systems, 43(6), pp. 1-15. https://doi.org/10.1007/s10916-019-1295-4.
16. Beaulac C, and Rosenthal JS. Predicting university students’ academic success and major using random forests. Research in Higher Education, 60, pp. 1048-1064. https://doi.org/10.1007/s11162-019-09546-y.
17. Boyer SSA. Transfer learning for predictive models in MOOCs (Doctoral dissertation, Massachusetts Institute of Technology).
18. Rivas A, Gonzalez-Briones A, Hernandez G, Prieto J, and Chamoso P. Artificial neural network analysis of the academic performance of students in virtual learning environments. Neurocomputing, 423, pp. 713-720. https://doi.org/10.1016/j.neucom.2020.02.125.
19. Yousafzai BK, Khan SA, Rahman T, Khan I, Ullah I, Ur Rehman A, Baz M, Hamam H, and Cheikhrouhou O. Student-performulator: student academic performance using hybrid deep neural network. Sustainability, 13(17), pp. 1-21. https://doi.org/10.3390/su13179775.
20. Dabhade P, Agarwal R, Alameen KP, Fathima AT, Sridharan R, and Gopakumar G. Educational data mining for predicting students’ academic performance using machine learning algorithms. Materials Today: Proceedings, 47, pp. 5260-5267. https://doi.org/10.1016/j.matpr.2021.05.646.
21. Baashar Y, Alkawsi G, Mustafa A, Alkahtani AA, Alsariera YA, Ali AQ, Hashim W, and Tiong SK. Toward predicting student’s academic performance using artificial neural networks (ANNs). Applied Sciences, 12(3), pp. 1-16. https://doi.org/10.3390/app12031289.
22. Imran M, Latif S, Mehmood D, and Shah MS. Student academic performance prediction using supervised learning techniques. International Journal of Emerging Technologies in Learning, 14(14), pp. 92-104.
23. Maheswari K, Priya A, Balamurugan A, and Ramkumar S. WITHDRAWN: Analyzing student performance factors using KNN algorithm. https://doi.org/10.1016/j.matpr.2020.12.1024.
24. Hasan R, Palaniappan S, Raziff ARA, Mahmood S, and Sarker KU. Student academic performance prediction by using decision tree algorithm. In 4th international conference on computer and information sciences (ICCOINS), pp. 1-5. https://doi.org/10.1109/ICCOINS.2018.8510600.
25. Rivas A, Gonzalez-Briones A, Hernandez G, Prieto J, and Chamoso P. Artificial neural network analysis of the academic performance of students in virtual learning environments. Neurocomputing, 423, pp. 713-720. https://doi.org/10.1016/j.neucom.2020.02.125.
26. Kuzilek J, Hlosta M, and Zdrahal Z. Open university learning analytics dataset. Scientific data, 4(1), pp. 1-8.
ETHICAL DECLARATIONS
No participation of humans takes place in this implementation process.
HUMAN AND ANIMAL RIGHTS
No violation of Human and Animal Rights is involved.
FINANCING
"The authors did not receive financing for the development of this research".
CONFLICT OF INTEREST
"The authors declare that there is no conflict of interest".
DATA AVAILABILITY
Based on the request authors can provide dataset details.
AUTHORSHIP CONTRIBUTION
Conceptualization: M. Viveka.
Data curation: M. Viveka.
Formal analysis: N.Shanmuga Priya.
Research: N.Shanmuga Priya.
Methodology: M. Viveka.
Drafting - original draft: N.Shanmuga Priya.
Writing - proofreading and editing: M. Viveka.